Question

已知集合A={（x，y）|y=2x²，x∈R}，B={（x，y）|y=2^x，x∈R}，则集合A∩B的真子集的个数为（　　）

A．3

B．4

C．7

D．8

Answer 1

分析：在同一坐标系中作出y=2x²和y=2^x的图象，观察图象，知y=2x²和y=2^x有三个不同的交点，所以集合A∩B中有三个元素，由此能求出集合A∩B的真子集的个数．

解答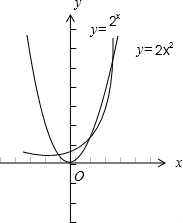：解：∵A={（x，y）|y=2x²，x∈R}，
B={（x，y）|y=2^x，x∈R}，
∴集合A∩B={（x，y）|

y=2x2 y=2x

}
在同一坐标系中作出y=2x²和y=2^x的图象，
观察图象，知y=2x²和y=2^x有三个不同的交点，
∴集合A∩B中有三个元素，
∴集合A∩B的真子集的个数为2³-1=7个．
故选C．

点评：本题考查指数函数的图象和性质，是基础题，解题时要认真审题，仔细解答，注意数形结合思想的灵活运用．