题目内容
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分。假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() 且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量ε分布列;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
(Ⅰ)ε的分布列为
| ε | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
(Ⅱ) ![]()
解析:
(Ⅰ)由题意知,ε的可能取值为0,1,2,3,且
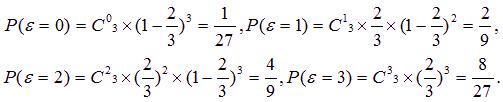
所以ε的分布列为
| ε | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
(Ⅱ)用C表示“甲得2分乙得1分”这一事件,用D表示“甲得3分乙得0分”这一事件,所以AB=C∪D,且C、D互斥,又
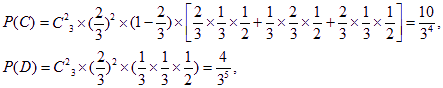
由互斥事件的概率公式得
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
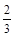 ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为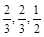 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响.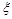 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量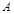 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为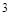 ”,用
”,用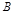 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求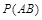 .
.