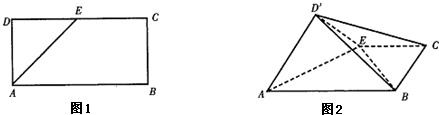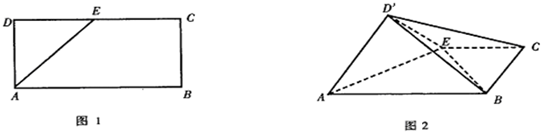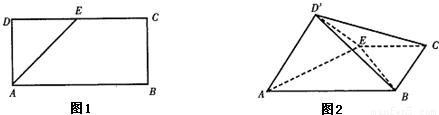题目内容
如图1,已知矩形ABCD,AB=2AD=2a,E是CD边的中点,以AE为棱,将△DAE向上折起,将D变到D′的位置,使面D′AE与面ABCE成直二面角(图2).(1)求直线D′B与平面ABCE所成的角的正切值;
(2)求证:AD′⊥BE;
(4)求异面直线AD′与BC所成的角.
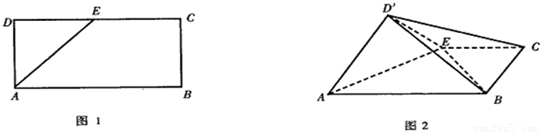
【答案】分析:(1)根据二面角的定义,作D′O⊥AE于O,连 OB,可得∠D′BO是直线D′B与平面ABCE所成的角,解直角△D′OB,即可求出直线D′B与平面ABCE所成的角的正切值;
(2)连接BE,则BE⊥AE于E,由线面垂直的性质,由(1)中结论D′O⊥平面ABCE,可得D′O⊥BE,结合线面垂直的判定定理,证得BE⊥平面AD′E后,易得AD′⊥BE;
(3)求异面直线AD′与BC所成的角,关键是作出线线角,作AK∥BC交CE的延长线于K,则∠D′AK是异面直线AD′与BC所成的角
解答:解:(1)∵D′-AE-B是直二面角,
∴平面D′AE⊥平面ABCE.
作D′O⊥AE于O,连 OB,则D′O⊥平面ABCE.
∴∠D′BO是直线D′B与平面ABCE所成的角.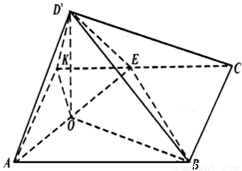
∵D′A=D′E=a,且D′O⊥AE于O,∠AD′E=90°
∴O是AE的中点,
AO=OE=D′O=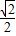 a,∠D′AE=∠BAO=45°.
a,∠D′AE=∠BAO=45°.
∴在△OAB中,OB=
=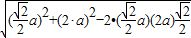 =
=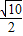 a.
a.
∴在直角△D′OB中,tan∠D′BO=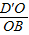 =
=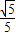 .
.
(2)如图,连接BE,
∵∠AED=∠BEC=45°,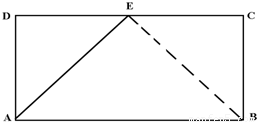
∴∠BEA=90°,
即BE⊥AE于E.
∵D′O⊥平面ABCE,
∴D′O⊥BE,
∴BE⊥平面AD′E,
∴BE⊥AD′.
(3)作AK∥BC交CE的延长线于K,
∴∠D′AK是异面直线AD′与BC所成的角,
∵四边形ABCK是矩形,
∴AK=BC=EK=a.
连接OK,D′K,
∴OK=D′O=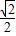 a,∠D′OK=90°,∴D′K=a,AK=AD′=D′K=a.
a,∠D′OK=90°,∴D′K=a,AK=AD′=D′K=a.
∴△D′AK是正三角形,∴∠D′AK=60°,
即异面直线AD′与BC成60°
点评:本题考查的知识点是直线与平面所成的角,空间中直线与直线之间的位置关系,点到平面的距离计算,其中(1)的关键是确定∠D′BO是直线D′B与平面ABCE所成的角,(2)的关键是熟练掌握空间中线线垂直与线面垂直之间的相互转化,(3)的关键是作出线线角.
(2)连接BE,则BE⊥AE于E,由线面垂直的性质,由(1)中结论D′O⊥平面ABCE,可得D′O⊥BE,结合线面垂直的判定定理,证得BE⊥平面AD′E后,易得AD′⊥BE;
(3)求异面直线AD′与BC所成的角,关键是作出线线角,作AK∥BC交CE的延长线于K,则∠D′AK是异面直线AD′与BC所成的角
解答:解:(1)∵D′-AE-B是直二面角,
∴平面D′AE⊥平面ABCE.
作D′O⊥AE于O,连 OB,则D′O⊥平面ABCE.
∴∠D′BO是直线D′B与平面ABCE所成的角.

∵D′A=D′E=a,且D′O⊥AE于O,∠AD′E=90°
∴O是AE的中点,
AO=OE=D′O=
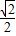 a,∠D′AE=∠BAO=45°.
a,∠D′AE=∠BAO=45°.∴在△OAB中,OB=

=
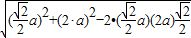 =
=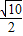 a.
a.∴在直角△D′OB中,tan∠D′BO=
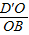 =
=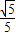 .
.(2)如图,连接BE,
∵∠AED=∠BEC=45°,

∴∠BEA=90°,
即BE⊥AE于E.
∵D′O⊥平面ABCE,
∴D′O⊥BE,
∴BE⊥平面AD′E,
∴BE⊥AD′.
(3)作AK∥BC交CE的延长线于K,
∴∠D′AK是异面直线AD′与BC所成的角,
∵四边形ABCK是矩形,
∴AK=BC=EK=a.
连接OK,D′K,
∴OK=D′O=
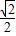 a,∠D′OK=90°,∴D′K=a,AK=AD′=D′K=a.
a,∠D′OK=90°,∴D′K=a,AK=AD′=D′K=a.∴△D′AK是正三角形,∴∠D′AK=60°,
即异面直线AD′与BC成60°
点评:本题考查的知识点是直线与平面所成的角,空间中直线与直线之间的位置关系,点到平面的距离计算,其中(1)的关键是确定∠D′BO是直线D′B与平面ABCE所成的角,(2)的关键是熟练掌握空间中线线垂直与线面垂直之间的相互转化,(3)的关键是作出线线角.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目