题目内容
已知数列{an}满足a1=1,且4an+1-anan+1+2an=9(n∈N*)。
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
(1)求a1,a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
解:(1)由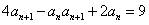 得
得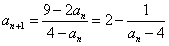 ,
,
求得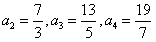 。
。
(2)猜想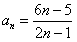 ;
;
证明:①当n=1时,猜想成立;
②设当n=k(k∈N*)时,猜想成立,即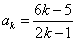 ,
,
则当n=k+1时,有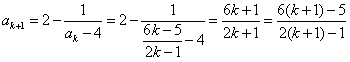 ,
,
所以,当n=k+1时猜想也成立;
综合①②,猜想对任何n∈N*都成立。
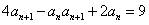 得
得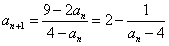 ,
,求得
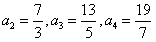 。
。(2)猜想
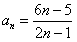 ;
;证明:①当n=1时,猜想成立;
②设当n=k(k∈N*)时,猜想成立,即
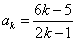 ,
,则当n=k+1时,有
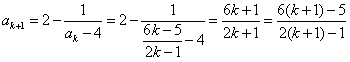 ,
,所以,当n=k+1时猜想也成立;
综合①②,猜想对任何n∈N*都成立。

练习册系列答案
相关题目