Question

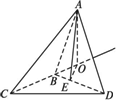
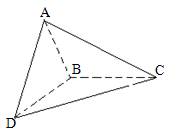
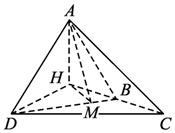
设△ABC和△DBC所在的两个平面互相垂直，且AB=BC=BD，∠ABC=∠DBC=，求:

(1)直线AD与平面BCD所成角的大小；

 (2)异面直线AD与BC所成的角；

(3)二面角A—BD—C的大小.

Answer 1

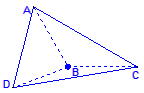
(1) 45° (2) AD与BC所成的角为90° (3) 二面角A—BD—C大小为π－arctan2.

解析:

(1)如图，在平面ABC内，过A作AH⊥BC，垂足为H，则AH⊥平面DBC，

∴∠ADH即为直线AD与平面BCD所成的角  由题设知△AHB≌△AHD，则DH⊥BH，AH=DH，

∴∠ADH=45°

 (2)∵BC⊥DH，且DH为AD在平面BCD上的射影，

∴BC⊥AD，故AD与BC所成的角为90°。

(3)过H作HR⊥BD，垂足为R，连结AR，则由三垂线定理知，AR⊥BD，故∠ARH为二面角A—BD—C的平面角的补角  设BC=a,则由题设知，AH=DH=,在△HDB中，HR=a，∴tanARH==2

故二面角A—BD—C大小为π－arctan2.

另法（向量法）: (略)