题目内容

12、设α、β为两个不同的平面，l、m为两条不同的直线，且l?α，m?β，有如下的两个命题：①若α∥β，则l∥m；②若l⊥m，则α⊥β．那么
①②
是假命题．
分析：根据m，l为两条不同的直线，α，β为两个不同的平面，可得该直线与直线可以平行，相交或异面，平面与平面平行或相交，把平面和直线放在长方体中，逐个排除易寻到答案．
解答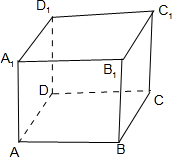：解：在长方体ABCD-A1B1C1D1中，
①、若平面AC是平面α，平面A1C1是平面β，
直线AD是直线l，A1B1是直线m，
显然满足l?α，m?β，α∥β，但是m与l异面；
故命题①是假命题；
②、若平面AC是平面α，平面AC1是平面β，
直线AB是直线l，AD1是直线m，
显然满足l?α，m?β，l⊥m，
但是α与β不垂直．
故②是假命题．
故答案为无，①②．
点评：此题是个基础题．考查直线与平面的位置关系，属于探究性的题目，要求学生对基础知识掌握必须扎实并能灵活应用，解决此题问题，可以把图形放入长方体中分析，体现了数形结合的思想和分类讨论的思想．
练习册系列答案
相关题目
4、设a、b为两条不同的直线，α、β为两个不同的平面．下列命题中，正确的是（　　）
设l，m，n为三条不同的直线，α，β为两个不同的平面，下列命题中正确的个数是（　　）
（1）若l∥m，m∥n，l⊥α，则n⊥α；          
（2）若m∥β，α⊥β，l⊥α，则l⊥m；
（3）若m?α，n?α，l⊥m，l⊥n，则l⊥α；    
（4）若l∥m，m⊥α，n⊥α，则l⊥n．
设l，m为两条不同的直线，α，β为两个不同的平面，下列命题中正确的是
②④
②④
．（填序号）
①若l⊥α，m∥β，α⊥β，则l⊥m；
②若l∥m，m⊥α，l⊥β，则α∥β；
③若l∥α，m∥β，α∥β，则l∥m；
④若α⊥β，α∩β=m，l?β，l⊥m，则l⊥α．
设α、β为两个不同的平面，m、n为两条不同的直线，且m?α，n?β，有如下的两个命题：p：若α∥β，则m∥n；q：若m⊥n，则α⊥β．那么（　　）
在平面内，设A，B为两个不同的定点，动点P满足：
PA
•
PB
=k2（k为实常数），则动点P的轨迹为（　　）
A、圆B、椭圆C、双曲线D、不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网