题目内容
双曲线C: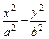 ="1" (a>0,b>0)的右顶点为A,x轴上有一点Q(2a,0),若C上存在一点P,使
="1" (a>0,b>0)的右顶点为A,x轴上有一点Q(2a,0),若C上存在一点P,使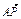 ·
·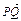 =0,求此双曲线离心率的取值范围.
=0,求此双曲线离心率的取值范围.
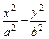 ="1" (a>0,b>0)的右顶点为A,x轴上有一点Q(2a,0),若C上存在一点P,使
="1" (a>0,b>0)的右顶点为A,x轴上有一点Q(2a,0),若C上存在一点P,使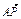 ·
·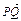 =0,求此双曲线离心率的取值范围.
=0,求此双曲线离心率的取值范围.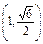
设P点坐标为(x,y),
则由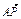 ·
·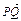 =0,得AP⊥PQ,
=0,得AP⊥PQ,
则P点在以AQ为直径的圆上,
即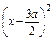 +y2=
+y2=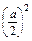 ①
①
又P点在双曲线上,得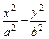 ="1 " ②
="1 " ②
由①,②消去y,得
(a2+b2)x2-3a3x+2a4-a2b2=0.
即[(a2+b2)x2-(2a3-ab2)](x-a)=0.
当x=a时,P与A重合,不符合题意,舍去.
当x=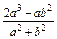 时,满足题意的P点存在,
时,满足题意的P点存在,
需x=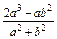 >a,化简得a2>2b2,
>a,化简得a2>2b2,
即3a2>2c2,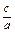 <
<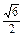 .∴离心率e=
.∴离心率e=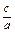 ∈
∈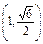 .
.
则由
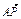 ·
·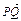 =0,得AP⊥PQ,
=0,得AP⊥PQ,则P点在以AQ为直径的圆上,
即
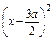 +y2=
+y2=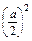 ①
①又P点在双曲线上,得
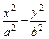 ="1 " ②
="1 " ②由①,②消去y,得
(a2+b2)x2-3a3x+2a4-a2b2=0.
即[(a2+b2)x2-(2a3-ab2)](x-a)=0.
当x=a时,P与A重合,不符合题意,舍去.
当x=
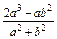 时,满足题意的P点存在,
时,满足题意的P点存在,需x=
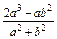 >a,化简得a2>2b2,
>a,化简得a2>2b2,即3a2>2c2,
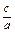 <
<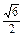 .∴离心率e=
.∴离心率e=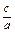 ∈
∈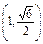 .
.
练习册系列答案
相关题目
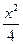 -y2=1的两个焦点分别为F1、F2,点P在双曲线上且满足∠F1PF2=90°,则△F1PF2的面积是___________.
-y2=1的两个焦点分别为F1、F2,点P在双曲线上且满足∠F1PF2=90°,则△F1PF2的面积是___________.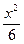 -
-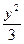 =1的焦点为F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为( )
=1的焦点为F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为( )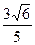
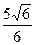
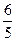
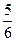
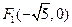 、
、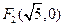 ,离心率
,离心率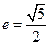 .(1)求双曲线的标准方程;(2)设
.(1)求双曲线的标准方程;(2)设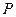 是(1)中所求双曲线上任意一点,过点
是(1)中所求双曲线上任意一点,过点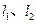 分别交于点
分别交于点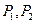 ,若
,若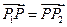 ,求
,求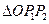 的面积.
的面积. 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.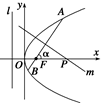
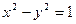 的一条弦的中点是(1,2),此弦所在的直线方程是__________________。
的一条弦的中点是(1,2),此弦所在的直线方程是__________________。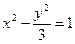 的两个焦点分别为F1、F2,点P为双曲线上一点,∠F1PF2=90°,则△F1PF2的面积等于( )
的两个焦点分别为F1、F2,点P为双曲线上一点,∠F1PF2=90°,则△F1PF2的面积等于( )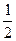
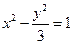 的右焦点F作直线l与双曲线C交于P、Q两点,
的右焦点F作直线l与双曲线C交于P、Q两点,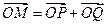 ,求点M的轨迹方程.
,求点M的轨迹方程.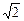 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.