题目内容
y=kx+2与x2+ =1交于A、B两点,且kOA+kOB=3,则直线AB的方程为
=1交于A、B两点,且kOA+kOB=3,则直线AB的方程为
- A.2x-3y-4=0
- B.2x+3y-4=0
- C.3x+2y-4=0
- D.3x-2y-4=0
C
分析:将y=kx+2代入x2+ =1,化为关于x的一元二次方程,利用根与系数的关系 及 kOA+kOB=3求出k值,即得直线AB的方程.
=1,化为关于x的一元二次方程,利用根与系数的关系 及 kOA+kOB=3求出k值,即得直线AB的方程.
解答:∵y=kx+2与 x2+ =1交于A、B两点,联立方程组可得 (2+k2)x2+4kx+2=0,
=1交于A、B两点,联立方程组可得 (2+k2)x2+4kx+2=0,
∴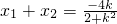 ,x1x2=
,x1x2=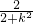 .
.
∵kOA+kOB=3,∴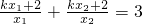 ,∴( 2k-3)x1x2+2 (x1+x2)=0,
,∴( 2k-3)x1x2+2 (x1+x2)=0,
∴( 2k-3)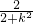 +2•
+2•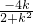 =0,∴k=-
=0,∴k=- ,故y=kx+2 即 y=-
,故y=kx+2 即 y=- x+2,
x+2,
即 3x+2y-4=0,
故选C.
点评:本题考查一元二次方程根与系数的关系,直线和圆相交的性质,由kOA+kOB=3求出k值,是解题的关键.
分析:将y=kx+2代入x2+
 =1,化为关于x的一元二次方程,利用根与系数的关系 及 kOA+kOB=3求出k值,即得直线AB的方程.
=1,化为关于x的一元二次方程,利用根与系数的关系 及 kOA+kOB=3求出k值,即得直线AB的方程.解答:∵y=kx+2与 x2+
 =1交于A、B两点,联立方程组可得 (2+k2)x2+4kx+2=0,
=1交于A、B两点,联立方程组可得 (2+k2)x2+4kx+2=0,∴
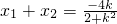 ,x1x2=
,x1x2=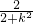 .
.∵kOA+kOB=3,∴
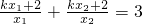 ,∴( 2k-3)x1x2+2 (x1+x2)=0,
,∴( 2k-3)x1x2+2 (x1+x2)=0,∴( 2k-3)
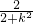 +2•
+2•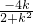 =0,∴k=-
=0,∴k=- ,故y=kx+2 即 y=-
,故y=kx+2 即 y=- x+2,
x+2,即 3x+2y-4=0,
故选C.
点评:本题考查一元二次方程根与系数的关系,直线和圆相交的性质,由kOA+kOB=3求出k值,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线y=kx+2与双曲线x2-y2=6只有一个交点,那么实数k的值是( )
A、
| ||||
B、±
| ||||
| C、±1 | ||||
D、±
|
y=kx+2与x2+
=1交于A、B两点,且kOA+kOB=3,则直线AB的方程为( )
| y2 |
| 2 |
| A、2x-3y-4=0 |
| B、2x+3y-4=0 |
| C、3x+2y-4=0 |
| D、3x-2y-4=0 |
 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,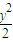 =1交于A、B两点,且kOA+kOB=3,则直线AB的方程为( )
=1交于A、B两点,且kOA+kOB=3,则直线AB的方程为( )