题目内容
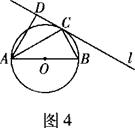
 如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.
如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.(1)求∠DAC的大小及线段AE的长;
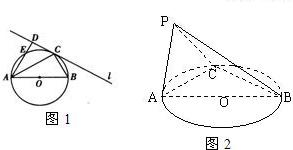
(2)如图2所示,将△ACD沿AC折起,点D折至点P处,且使得△ACP所在平面与圆O所在平面垂直,连接BP,求二面角P-AB-C大小的余弦值.
分析:(1)连接OC,则OC∥AD,根据Rt△AEB≌Rt△BCA,即可求出AE的值;
(2)过P作PH⊥AC于H,过H作HF⊥AB于F,连接PF,则PF⊥AB,故∠PFH为二面角P-AB-C的平面角,在Rt△APC中,求出PH,根据勾股定理求出AH,在Rt△AFH中,求出∠PFH的余弦值.
(2)过P作PH⊥AC于H,过H作HF⊥AB于F,连接PF,则PF⊥AB,故∠PFH为二面角P-AB-C的平面角,在Rt△APC中,求出PH,根据勾股定理求出AH,在Rt△AFH中,求出∠PFH的余弦值.
解答:解:(1)连接OC,则OC∥AD,CB=OB=OC,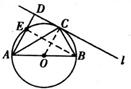
∴∠COB=∠EAO=60°,∠CAO=30°,
∴Rt△AEB≌Rt△BCA,
∴CB=AE=3.(5分)
(2)过P作PH⊥AC于H,由于平面PAC⊥平面⊙O,则PH⊥平面⊙O.
过H作HF⊥AB于F,连接PF,则PF⊥AB,故∠PFH为二面角P-AB-C的平面角.(8分)
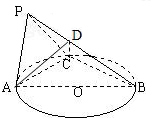 在Rt△APC中,PH=AP•sin30°=AC•cos30°•sin30°=3
在Rt△APC中,PH=AP•sin30°=AC•cos30°•sin30°=3
×
×
=
,
AP2=AH•AC得AH=
=
,
在Rt△AFH中,FH=AHsin30°=
,
故tan∠PFH=
=
=
.故cos∠PFH=
.(12分)

∴∠COB=∠EAO=60°,∠CAO=30°,
∴Rt△AEB≌Rt△BCA,
∴CB=AE=3.(5分)
(2)过P作PH⊥AC于H,由于平面PAC⊥平面⊙O,则PH⊥平面⊙O.
过H作HF⊥AB于F,连接PF,则PF⊥AB,故∠PFH为二面角P-AB-C的平面角.(8分)
 在Rt△APC中,PH=AP•sin30°=AC•cos30°•sin30°=3
在Rt△APC中,PH=AP•sin30°=AC•cos30°•sin30°=3| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
AP2=AH•AC得AH=
| AP2 |
| AC |
9
| ||
| 4 |
在Rt△AFH中,FH=AHsin30°=
9
| ||
| 8 |
故tan∠PFH=
| PH |
| PF |
| ||||
|
2
| ||
| 3 |
| ||
| 7 |
点评:本题主要考查了与二面角有关的立体几何综合题,考查对基础知识的综合应用能力和基本定理的掌握能力.

练习册系列答案
相关题目

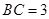 过
过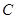 作圆的切线
作圆的切线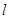 ,过A作
,过A作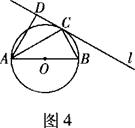
 如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.
如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.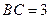 过
过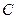 作圆的切线
作圆的切线 ,过A作
,过A作