题目内容
设关于x的方程sinx+| 3 |
(1)求α的取值范围.(2)求tan(α+β)的值.
分析:(Ⅰ)通过两角和公式对方程进行化简,因有相异二解推断出sin(x+
)不等于sin
和±1,进而推断|-
|<1,求出a的取值范围.
(Ⅱ)把方程的相异解α、β分别代入方程,得到的两个方程相减,求得tan
的值,再用二倍角公式求出tan(α+β)的值.
| π |
| 3 |
| π |
| 3 |
| a |
| 2 |
(Ⅱ)把方程的相异解α、β分别代入方程,得到的两个方程相减,求得tan
| α+β |
| 2 |
解答:解:(Ⅰ)∵sinx+
cosx=2(
sinx+
cosx)=2sin(x+
),
∴方程化为sin(x+
)=-
.
∵方程sinx+
cosx+a=0在(0,2π)内有相异二解,
∴sin(x+
)≠sin
=
.
又sin(x+
)≠±1(∵当等于
和±1时仅有一解),
∴|-
|<1.且-
≠
.即|a|<2且a≠-
.
∴a的取值范围是(-2,-
)∪(-
,2).
(Ⅱ)∵α、β是方程的相异解,
∴sinα+
cosα+a=0①.
sinβ+
cosβ+a=0②.
①-②得(sinα-sinβ)+
(cosα-cosβ)=0.
∴2sin
cos
-2
sin
sin
=0,又sin
≠0,
∴tan
=
.
∴tan(α+β)=
=
.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴方程化为sin(x+
| π |
| 3 |
| a |
| 2 |
∵方程sinx+
| 3 |
∴sin(x+
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
又sin(x+
| π |
| 3 |
| ||
| 2 |
∴|-
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| 3 |
∴a的取值范围是(-2,-
| 3 |
| 3 |
(Ⅱ)∵α、β是方程的相异解,
∴sinα+
| 3 |
sinβ+
| 3 |
①-②得(sinα-sinβ)+
| 3 |
∴2sin
| α-β |
| 2 |
| α+β |
| 2 |
| 3 |
| α+β |
| 2 |
| α-β |
| 2 |
| α+β |
| 2 |
∴tan
| α+β |
| 2 |
| ||
| 3 |
∴tan(α+β)=
2tan
| ||
1-tan2
|
| 3 |
点评:本题主要考查三角函数中的两角和公式.解题的关键既要熟练掌握公式,又要灵活利用特殊角.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
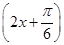 =
=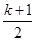 在
在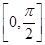 内有两个不同根α、β,求α+β的值及k的取值范围.
内有两个不同根α、β,求α+β的值及k的取值范围.