题目内容
设f(n,p)=C2np(n,p∈N,p≤2n).数列{a(n,p)}满足a(1,p)+a(2,p)+…+a(n,p)=f(n,p).
(1)求证:{a(n,2)}是等差数列;
(2)求证:f(n,1)+f(n,2)+…+f(n,n)=22n-1+
C2nn-1;
(3)设函数H(x)=f(n,1)x+f(n,2)x2+…+f(n,2n)x2n,试比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小.
(1)求证:{a(n,2)}是等差数列;
(2)求证:f(n,1)+f(n,2)+…+f(n,n)=22n-1+
| 1 | 2 |
(3)设函数H(x)=f(n,1)x+f(n,2)x2+…+f(n,2n)x2n,试比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小.
分析:(1)由a(1,p)+a(2,p)+…+a(n,p)=f(n,p),令p=2,得a(1,2)+a(2,2)+…+a(n,2)=f(n,2),
a(1,2)+a(2,2)+…+a(n-1,2)=f(n-1,2)(n≥2,且n∈N*),由此能导出{a(n,2)}是等差数列.
(2)设f(n,1)+f(n,2)+…+f(n,n)=C2n1+C2n2+…+C2nn=S,而C2n0+C2n1+C2n2+C2n2n=22n,由此能够证明:S=22n-1+
C2nn-1.
(3)H(x)=f(n,1)x+f(n,2)x2+…+f(n,2n)x2n,=(1+x)2n-1,所以H(x)-H(a)=(1+x)2n-(1+a)2n.
为了比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小,即要判断(1+x)2n-(1+a)2n-2n(1+a)2n-1(x-a)的符号.由此能够比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小.
a(1,2)+a(2,2)+…+a(n-1,2)=f(n-1,2)(n≥2,且n∈N*),由此能导出{a(n,2)}是等差数列.
(2)设f(n,1)+f(n,2)+…+f(n,n)=C2n1+C2n2+…+C2nn=S,而C2n0+C2n1+C2n2+C2n2n=22n,由此能够证明:S=22n-1+
| 1 |
| 2 |
(3)H(x)=f(n,1)x+f(n,2)x2+…+f(n,2n)x2n,=(1+x)2n-1,所以H(x)-H(a)=(1+x)2n-(1+a)2n.
为了比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小,即要判断(1+x)2n-(1+a)2n-2n(1+a)2n-1(x-a)的符号.由此能够比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小.
解答:解:(1)由a(1,p)+a(2,p)+…+a(n,p)=f(n,p),
令p=2,得
a(1,2)+a(2,2)+…+a(n,2)=f(n,2),
a(1,2)+a(2,2)+…+a(n-1,2)=f(n-1,2)(n≥2,且n∈N*),
两式相减,得a(n,2)=C2n2-C2(n-1)2=4n-3,
且n=1时也成立.
所以a(n+1,2)-a(n,2)=4,
即{a(n,2)}是等差数列. (5 分)
(2)设f(n,1)+f(n,2)+…+f(n,n)
=C2n1+C2n2+…+C2nn=S,
而C2n0+C2n1+C2n2+C2n2n=22n,
又C2n2n-1=C2n1,C2n2n-2=C2n2,…,C2nn=C2nn,
所以2S+2C2nn=22n,
所以S=22n-1+
C2nn-1.(10分)
(3)H(x)=f(n,1)x+f(n,2)x2+…+f(n,2n)x2n
=(1+x)2n-1,
所以H(x)-H(a)=(1+x)2n-(1+a)2n.
为了比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小,
即要判断(1+x)2n-(1+a)2n-2n(1+a)2n-1(x-a)的符号.
设X=1+x,A=1+a,
则上式即为X2n-A2n-2nA2n-1(X-A),
设F(X)=X2n-A2n-2nA2n-1(X-A),
其导数为F′(X)=2nX2n-1-2nA2n-1=2n(X2n-1-A2n-1).
当X≥A时,F′(X)≥0,
则F(X)是增函数,
所以F(X)≥F(A),
且当X=A时等号成立.
当X<A时,F′(X)<0,
则F(X)是减函数,
所以F(X)>F(A).
纵上所述,H(x)-H(a)≥2n(1+a)2n-1(x-a),
当且仅当x=a时等号成立.
令p=2,得
a(1,2)+a(2,2)+…+a(n,2)=f(n,2),
a(1,2)+a(2,2)+…+a(n-1,2)=f(n-1,2)(n≥2,且n∈N*),
两式相减,得a(n,2)=C2n2-C2(n-1)2=4n-3,
且n=1时也成立.
所以a(n+1,2)-a(n,2)=4,
即{a(n,2)}是等差数列. (5 分)
(2)设f(n,1)+f(n,2)+…+f(n,n)
=C2n1+C2n2+…+C2nn=S,
而C2n0+C2n1+C2n2+C2n2n=22n,
又C2n2n-1=C2n1,C2n2n-2=C2n2,…,C2nn=C2nn,
所以2S+2C2nn=22n,
所以S=22n-1+
| 1 |
| 2 |
(3)H(x)=f(n,1)x+f(n,2)x2+…+f(n,2n)x2n
=(1+x)2n-1,
所以H(x)-H(a)=(1+x)2n-(1+a)2n.
为了比较H(x)-H(a)与2n(1+a)2n-1(x-a)的大小,
即要判断(1+x)2n-(1+a)2n-2n(1+a)2n-1(x-a)的符号.
设X=1+x,A=1+a,
则上式即为X2n-A2n-2nA2n-1(X-A),
设F(X)=X2n-A2n-2nA2n-1(X-A),
其导数为F′(X)=2nX2n-1-2nA2n-1=2n(X2n-1-A2n-1).
当X≥A时,F′(X)≥0,
则F(X)是增函数,
所以F(X)≥F(A),
且当X=A时等号成立.
当X<A时,F′(X)<0,
则F(X)是减函数,
所以F(X)>F(A).
纵上所述,H(x)-H(a)≥2n(1+a)2n-1(x-a),
当且仅当x=a时等号成立.
点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,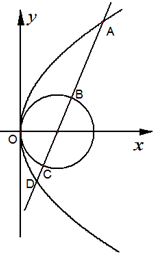 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).