题目内容
(本题满分13分)定义在R上的函数 满足:对任意实数
满足:对任意实数 ,总有
,总有 ,且当
,且当 时,
时, .
.
(1)试求 的值;
的值;
(2)判断 的单调性并证明你的结论;
的单调性并证明你的结论;
【答案】
解:(1)在 中,令
中,令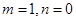 .得:
.得:
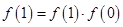 .
.
因为 ,所以,
,所以, .---------------4分
.---------------4分
(2)要判断 的单调性,可任取
的单调性,可任取 ,且设
,且设 .
.
在已知条件 中,若取
中,若取 ,则已知条件可化为:
,则已知条件可化为: .------------------------------7分
.------------------------------7分
由于 ,所以
,所以 .
.
为比较 的大小,只需考虑
的大小,只需考虑 的正负即可.
的正负即可.
在 中,令
中,令 ,
, ,则得
,则得 .
.
∵  时,
时, ,
,
∴ 当 时,
时, .-----------------------11分
.-----------------------11分
又 ,所以,综上,可知,对于任意
,所以,综上,可知,对于任意 ,均有
,均有 .
.
∴  .
.
∴ 函数 在R上单调递减.------------------------------13分
在R上单调递减.------------------------------13分
【解析】略

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 与直线
与直线 相切,且与定圆
相切,且与定圆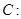
 外切,求动圆圆心
外切,求动圆圆心