题目内容

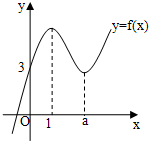函数f（x）=ax3+bx2+（c-3a-2b）x+d的图象如图所示．
（1）若函数f（x）在x=2处的切线方程为3x+y-11=0，求函数f（x）的解析式
（2）在（1）的条件下，是否存在实数m，使得y=f（x）的图象与y=
13
f′(x)+5x+m的图象有且只有三个不同的交点？若存在，求出m的取值范围；若不存在，说明理由．
分析：（1）由图象过点（0，3）求出d，再利用1是极值点求出c，利用切线的斜率为-3得f′（2）=-3且f（2）=5求出a，b即可得函数f（x）的解析式；
（2）由题意可得：x3-6x2+9x+3=x2+x+3+m有三个不相等的实根，等价于g（x）=x3-7x2+8x与y=m有三个不同的交点，利用导数可求函数的极大与极小，即可得m的取值范围．
解答：解：（1）由图可知函数f（x）的图象过点（0，3），且f′（1）=0，
∴
d=3
3a+2b+c-3a-2b=0
，
d=3
c=0
----3
依题意f′（2）=-3且f（2）=5，解得a=1，b=-6
所以f（x）=x3-6x2+9x+3----6
（2）由题意可得：x3-6x2+9x+3=x2+x+3+m有三个不相等的实根，
即g（x）=x3-7x2+8x与y=m有三个不同的交点g′（x）=3x2-14x+8=（3x-2）（x-4）

x (-∞，
2
3
)
2
3
 (
2
3
，4)		 4 （4，+∞）
g′（x） + 0 _ 0 +
g（x） 增 极大 减 极小 增
则g(
2
3
)=
68
27
，g（4）=-16，故m的取值范围是(-16，
68
27
)----12
点评：本题考查利用导数求函数的极值，及导数的几何意义，考查根的个数的应用和数形结合思想的应用．解题的关键是将方程根的问题转化为图象的交点问题．
练习册系列答案
相关题目
有下列命题：
①若f（x）存在导函数，则f′（2x）=[f（2x）]′．
②若函数h（x）=cos4x-sin4x，则h′(
π12
)=1；
③若函数g（x）=（x-1）（x-2）…（x-2009）（x-2010），则g′（2010）=2009!．
④若三次函数f（x）=ax3+bx2+cx+d，则“a+b+c=0”是“f（x）有极值点”的充要条件．
其中真命题的序号是
 
．
18、已知函数f（x）=ax3-6ax2+b（x∈[-1，2]）的最大值为3，最小值为-29，求a、b的值．
对于三次函数f（x）=ax3+bx2+cx+d（a≠0）．
定义：（1）设f″（x）是函数y=f（x）的导数y=f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”；
定义：（2）设x0为常数，若定义在R上的函数y=f（x）对于定义域内的一切实数x，都有f（x0+x）+f（x0-x）=2f（x0）成立，则函数y=f（x）的图象关于点（x0，f（x0））对称．
己知f（x）=x3-3x2+2x+2，请回答下列问题：
（1）求函数f（x）的“拐点”A的坐标
 
；
（2）检验函数f（x）的图象是否关于“拐点”A对称，对于任意的三次函数写出一个有关“拐点”的结论
 
．
若函数f（x）=ax3-2x2+a2x在x=1处有极小值，则实数a等于
1
1
．
已知下表为函数f（x）=ax3+cx+d部分自变量取值及其对应函数值，为了便于研究，相关函数值取非整数值时，取值精确到0.01．
x -0.61 -0.59 -0.56 -0.35 0 0.26 0.42 1.57 3.27
y 0.07 0.02 -0.03 -0.22 0 0.21 0.20 -10.04 -101.63
根据表中数据，研究该函数的一些性质：
（1）判断f（x）的奇偶性，并证明；
（2）判断f（x）在[0.55，0.6]上是否存在零点，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网