题目内容
已知P(-2,0,2),Q(-1,1,2),R(-3,0,4),设| a |
| PQ |
| b |
| PR |
| a |
| b |
| c |
分析:解出互相垂直的两向量的坐标,将垂直用内积为零表示出,得到参数k的方程,求k.
解答:解:由已知
=
=(1,1,0),
=
=(-1,0,2),故k
+
=(k-1,k,2)
∵k
+
与
=(2,1,-2)垂直,
∴(k
+
)•
=0
∴2k-2+k-4=0,得k=2
故应填2,
| a |
| PQ |
| b |
| PR |
| a |
| b |
∵k
| a |
| b |
| c |
∴(k
| a |
| b |
| c |
∴2k-2+k-4=0,得k=2
故应填2,
点评:本题考点是两向量垂直的条件,由向量垂直的条件建立方程求参数是这几年高考的热点.

练习册系列答案
相关题目
 =
= ,
, =
=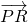 ,实数k使得k
,实数k使得k =(2,1,-2)垂直,则k的值为________.
=(2,1,-2)垂直,则k的值为________. =
= ,
, =
= ,实数k使得k
,实数k使得k +
+ 与
与 =(2,1,-2)垂直,则k的值为 .
=(2,1,-2)垂直,则k的值为 .