题目内容
如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.
直线l2的方程是x+y-3=0
解析:
设l2的方程为y=-x+b(b＞1),
则图中A(1,0),D(0,1),B(b,0),C(0,b).
∴|AD|=
,|BC|=
.
梯形的高h就是A点到直线l2的距离,
故
.
由梯形面积公式,得
,
∴b2=9,b=±3.但b＞1,∴b=3.
从而得到直线l2的方程是x+y-3=0
练习册系列答案
浙江名校名师金卷系列答案
相关题目
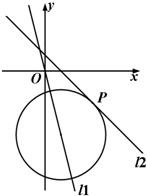如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．
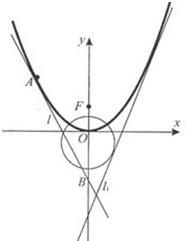如图，已知直线l1：y=2x+m（m＜0）与抛物线C1：y=ax2（a＞0）和圆C2：x2+（y+1）2=5都相切，F是C1的焦点．
如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．求有圆心在l1上且与直线l2相切于点P的圆的方程．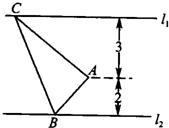
如图，已知直线l1∥l2，点A是l1，l2之间的定点，点A到l1，l2之间的距离分别为3和2，点B是l2上的一动点，作AC⊥AB，且AC与l1交于点C，则△ABC的面积的最小值为
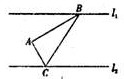如图，已知直线l1∥l2，点A是l1，l2上两直线之间的动点，且到l1距离为4，到l2距离为3，若