题目内容
（本小题满分12分）
已知二次函数f(x) 对任意x∈R，都有f (1-x)=f (1+x)成立，设向量a=(sinx,2), b=(2sinx,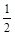
),c=(cos2x,1),d=(1,2)。
（1）分别求a·b和c·d的取值范围；
（2）当x∈[0,π]时，求不等式f(a·b)>f(c·d)的解集。
【答案】
(1）a·b=2sin2x+1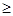
1 c·d=2cos2x+1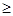1
（2）∵f(1-x)=f(1+x) ∴f(x)图象关于x=1对称
当二次项系数m>0时, f(x)在（1，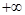
）内单调递增，
由f(a·b)>f(c·d)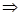
a·b
> c·d, 即2sin2x+1>2cos2x+1
又∵x∈[0,π] ∴x∈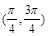
当二次项系数m<0时,f(x)在（1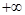，）内单调递减，
由f(a·b)>f(c·d)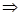 a·b
> c·d, 即2sin2x+1<2cos2x+1
又∵x∈[0,π] ∴x∈
、
故当m>0时不等式的解集为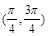;当m<0时不等式的解集为
【解析】略
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
