题目内容
（本小题12分）
已知函数f (x)＝2sinωx·cos(ωx＋
)＋
(ω>0)的最小正周期为4π.
（1）求正实数ω的值；
（2）在锐角△ABC中，内角A、B、C的对边分别为a、b、c，且满足
，求f (B)的值.
（12分）
（1）∵f(x)＝2sinωx(cosωx·cos－sinωx·sin)＋(2分)
＝
sinωxcosωx－sin2ωx＋＝
sin2ωx－(1－cos2ωx)＋＝sin(2ωx＋).(5分)
又f(x)的最小正周期T＝
＝4π，则ω＝
.(6分)
（2）由得到
所以
∴
∵△ABC为锐角三角形∴cosB=
∴
由(1)f(x)＝sin(
＋)，从而f(B)＝sin(
×＋)＝sin＝.(12分)
练习册系列答案
相关题目
，
，直线
与函数
、
的k*s#5^u图象都相切，且与函数
.
的k*s#5^u值；
(其中
是
的k*s#5^u最大值；
时，求证：
.
中，
。
中，
，求数列
项和
.
轴上的抛物线与直线
交于P、Q两点，|PQ|=
，求抛物线的方程
；
过
且与圆C相切，求直线
，使直线
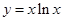
处的切线方程。