题目内容
已知函数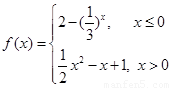 .
.
(1)写出该函数的单调区间;
(2)若函数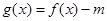 恰有3个不同零点,求实数
恰有3个不同零点,求实数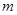 的取值范围;
的取值范围;
(3)若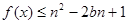 对所有
对所有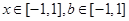 恒成立,求实数n的取值范围。
恒成立,求实数n的取值范围。
【答案】
(1)单调增区间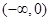 ,
,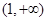 单调递减区间是
单调递减区间是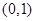
(2)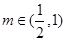 (3)n的取值范围是
(3)n的取值范围是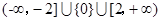
【解析】
试题分析:(1) 由函数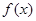 的图象 函数
的图象 函数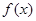 的单调递减区间是
的单调递减区间是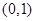
单调增区间是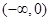 ,
,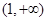
(2)作出直线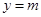 ,
,
函数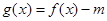 恰有3个不同零点等价于函数
恰有3个不同零点等价于函数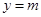
与函数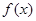 的图象恰有三个不同公共点。结合图形
的图象恰有三个不同公共点。结合图形
且函数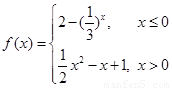 又 f(0)="1" f(1)=
又 f(0)="1" f(1)=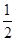
∴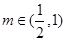
(3) 解:若要使f (x)≤n2-2bn+1对所有x∈[-1,1]恒成立
则需 [f(x)]max≤n2-2bn+1 [f(x)]max=f(0)=1
∴n2-2bn+1≥1即n2-2bn≥0在b∈[-1,1]恒成立
∴y= -2nb+n2在b∈[-1,1]恒大于等于0
∴ ,∴
,∴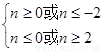
∴n的取值范围是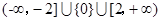
考点:函数图象的作法;函数的单调性及单调区间;根的存在性及根的个数判断.恒成立问题.
点评:本题考查了函数图象的作法、函数的单调性及函数零点问题,本题的解决过程充分体现了数形结合
思想的作用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
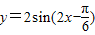 .
.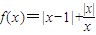 .
.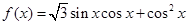 .
.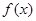 的最小正周期和单调增区间;
的最小正周期和单调增区间;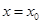 对称,且
对称,且 ,求
,求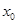 的值.
的值.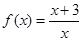 :
: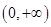 为单调递减函数;
为单调递减函数;
 的奇偶性.
的奇偶性.