题目内容
棱长为
的正方体各个面的中心连线构成一个几何体，该几何体的体积为（ ）
A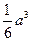． | B． | C． | D． |
A
解析
练习册系列答案
相关题目
）
．
中，已知面
是边长为3的正方形，
与面
中，若
、
分别为
、
的中点，平面
将三棱柱分成体积为
、
的两部分，那么
为（ ）
正三棱柱的底面边长为3，高为2，则其外接球的表面积为（ ）
| A． 4π | B． π | C． π | D．16π |
C三点，如果AB=AC=2，BC=2
，则球心到平面ABC的距离为 （ ）
C．用与
球心距离为1的平面截球体，所得截面面积为
，则该球体的体积为 （ ）
A． | B．4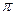 | C． | D． |
题目内容
棱长为的正方体各个面的中心连线构成一个几何体，该几何体的体积为（ ）
| A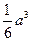． | B． | C． | D． |
A
解析
正三棱柱的底面边长为3，高为2，则其外接球的表面积为（ ）
| A． 4π | B．π | C．π | D．16π |
用与球心距离为1的平面截球体，所得截面面积为，则该球体的体积为 （ ）
| A． | B．4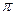 | C． | D． |