Question

（2012•西区模拟）如图，三棱锥P-ABC中，PA⊥平面ABC，PA=2，△ABC是边长为

3

的正三角形，点D是PB的中点，则异面直线PA与CD所成角的正切值为（　　）

• A．

  2

  3

• B．

  3

  2

• C．

  1

  3

• D．

  1

  2

Answer 1

分析：取AB中点E，连接CE，由三角形中位线定理，证明DE∥PA，从而证明∠CDE为PA与CD所成的角，最后在Rt△DEC中计算此角的正切值即可

解答：解：如图，取AB中点E，连接CE，DE，则DE∥PA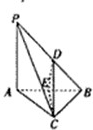
∴∠CDE为PA与CD所成的角
∵PA⊥平面ABC，∴DE⊥平面ABC，∴DE⊥EC
在Rt△DEC中，DE=

PA

2

=1，CE=

3

2

AB=

3

2

，
∴tan∠CDE=

CE

DE

=

3

2

故选B

点评：本题主要考查了空间异面直线所成的角的作法、证法、算法，将空间问题转化为平面问题的思想方法，属基础题