题目内容
用反证法证明命题“对任意a、b∈R，a2+b2≥2（a-b-1）”，正确的反设为
存在a，b∈R，a2+b2＜2（a-b-1）
存在a，b∈R，a2+b2＜2（a-b-1）
．分析：根据反证法的思想，反设出结论的否定成立即可得到正确答案
解答：解：反证法是在条件不变，利用结论的否定为条件进行推理找出矛盾
所以用反证法证明命题“对任意a、b∈R，a2+b2≥2（a-b-1）”，正确的反设是“存在a，b∈R，a2+b2＜2（a-b-1）”，
故答案为：存在a，b∈R，a2+b2＜2（a-b-1）
所以用反证法证明命题“对任意a、b∈R，a2+b2≥2（a-b-1）”，正确的反设是“存在a，b∈R，a2+b2＜2（a-b-1）”，
故答案为：存在a，b∈R，a2+b2＜2（a-b-1）
点评：本题考查反证法的思想，理解反证法的基本规则是解答的关键，本题是基础概念考查题，较易
练习册系列答案
阅读快车系列答案
相关题目
、
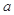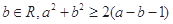”，正确的反设为 
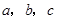中恰有一个偶数”正确的反设为( )
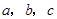中恰有一个偶数”正确的反设为( )