题目内容
已知函数
其中x∈R，
为参数，且
(1)当cos
＝0时，判断函数f(x)是否有极值；
(2)要使函数f(x)的极小值大于零，求参数
的取值范围；
(3)若对(2)中所求的取值范围内的任意参数
，函数f(x)在区间(2a－1，a)内都是增函数，求实数a的取值范围．
答案：
解析：
解析：
|
解：(1)解：当 (2)解： 由 当
因此，函数 要使 (3)由(2)知，函数 由题设，函数 由(Ⅱ)，参数 |
时
则
在
内是增函数，故无极值． 3分
令
得
及(I)，只需考虑
的情况．
变化时，
的符号及
处取得极小值
且
必有
可得
所以
8分
与
内都是增函数．
内是增函数，则
须满足不等式组
或
时，
要使不等式
关于参数
恒成立，必有
综上，解得
或
所以
14分
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
其中x∈R，则下列结论中正确的是
向左平移
个单位得到函数f(x)的图象
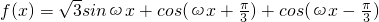，x∈R，（其中ω＞0）．
，则当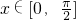
时，求f（x）的单调递减区间．
，x∈R，（其中ω＞0）．
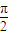，则当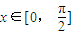
时，求f（x）的单调递减区间．
（x∈R）的图象为曲线C．