题目内容
定义在R上的f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,α,β是钝角三角形的两锐角,则下列正确的个数是( )
①f(sinβ)<f(cosα);
②f(sin(-α)<f(cosβ);
③f(cosα)>f(sin(-β));
④f(sinα)>f(cosβ).
①f(sinβ)<f(cosα);
②f(sin(-α)<f(cosβ);
③f(cosα)>f(sin(-β));
④f(sinα)>f(cosβ).
| A、4个 | B、3个 | C、2个 | D、1个 |
分析:本题考查的是函数的单调性、分段函数以及有关三角的综合类问题.在解答时,首先要结合分类讨论研究好当x∈[3,5]时,f(x)的解析式,画出图象后再结合周期性将整个实属集上的图象画出,结合图象即可读出奇偶性又可知道函数在(0,1)上的单调性,进而问题即可获得解答.
解答: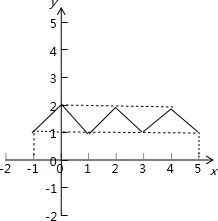 解:由题意函数f(x)的解析式为:
解:由题意函数f(x)的解析式为:
f(x)=
,
又因为在R上的f(x)满足f(x)=f(x+2),
所以函数是以2为周期的函数.
故函数在实数集上的图象如图,
由图象可知:函数为偶函数且在(0,1)上为减函数.
所以:∵α+β<
,
∴α<
-β或β<
-α
∴sinα<sin(
-β) =cosβ,同理sinβ<cosα
所以:f(sinα)>f(cosβ)、f(sinβ)>f(cosα)
又知函数为偶函数,∴f(sin(-α))f(-sinα)=f(sinα),f(sin(-β))=f(sinβ)
所以①②③不正确.
故选D.
 解:由题意函数f(x)的解析式为:
解:由题意函数f(x)的解析式为:f(x)=
|
又因为在R上的f(x)满足f(x)=f(x+2),
所以函数是以2为周期的函数.
故函数在实数集上的图象如图,
由图象可知:函数为偶函数且在(0,1)上为减函数.
所以:∵α+β<
| π |
| 2 |
∴α<
| π |
| 2 |
| π |
| 2 |
∴sinα<sin(
| π |
| 2 |
所以:f(sinα)>f(cosβ)、f(sinβ)>f(cosα)
又知函数为偶函数,∴f(sin(-α))f(-sinα)=f(sinα),f(sin(-β))=f(sinβ)
所以①②③不正确.
故选D.
点评:本题考查的是函数的单调性、分段函数以及有关三角的综合类问题.在解答的过程当中充分体现了分类讨论的思想、数形结合的思想以及函数单调性知识和周期性知识的灵活应用.值得同学们体会反思.

练习册系列答案
相关题目