题目内容
 已知正方形ABCD的边长为2
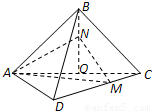
已知正方形ABCD的边长为2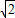 ,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )
,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )A.
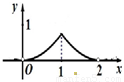
B.
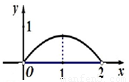
C.
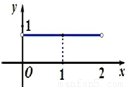
D.
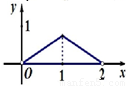
【答案】分析:先根据条件得到BO⊥平面ACD;进而求出三棱锥N-AMC的体积的表达式,即可求出结论.
解答:解:因为正方形ABCD的边长为2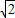 ,
,
所以:AC=4
又平面ABC⊥平面ACD,O为AC边的中点
∴BO⊥AC;
所以BO⊥平面ACD
∴三棱锥N-AMC的体积
y=f(x)= S△AMC•NO
S△AMC•NO
= ×
× AC•CM•sin∠ACM•NO
AC•CM•sin∠ACM•NO
= ×
× ×4•x•
×4•x•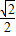 ×(2-x)
×(2-x)
=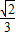 (-x2+2x)
(-x2+2x)
=-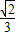 (x-1)2+
(x-1)2+
即为开口向下,对称轴为1的抛物线.
故选:B.
点评:本题主要考察棱柱、棱锥、棱台的体积计算.解决本题的关键在于先根据条件得到BO⊥平面ACD.
解答:解:因为正方形ABCD的边长为2
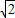 ,
,所以:AC=4
又平面ABC⊥平面ACD,O为AC边的中点
∴BO⊥AC;
所以BO⊥平面ACD
∴三棱锥N-AMC的体积
y=f(x)=
 S△AMC•NO
S△AMC•NO=
 ×
× AC•CM•sin∠ACM•NO
AC•CM•sin∠ACM•NO=
 ×
× ×4•x•
×4•x•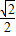 ×(2-x)
×(2-x)=
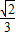 (-x2+2x)
(-x2+2x)=-
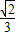 (x-1)2+
(x-1)2+
即为开口向下,对称轴为1的抛物线.
故选:B.
点评:本题主要考察棱柱、棱锥、棱台的体积计算.解决本题的关键在于先根据条件得到BO⊥平面ACD.

练习册系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.