题目内容
设a为实数,函数f(x)=2x2+(x-a)|x-a|.(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.
分析:(1)f(0)≥1?-a|a|≥1再去绝对值求a的取值范围,
(2)分x≥a和x<a两种情况来讨论去绝对值,再对每一段分别求最小值,借助二次函数的对称轴及单调性.最后综合即可.
(3)h(x)≥1转化为3x2-2ax+a2-1≥0,因为不等式的解集由对应方程的根决定,所以再对其对应的判别式分三种情况讨论求得对应解集即可.
(2)分x≥a和x<a两种情况来讨论去绝对值,再对每一段分别求最小值,借助二次函数的对称轴及单调性.最后综合即可.
(3)h(x)≥1转化为3x2-2ax+a2-1≥0,因为不等式的解集由对应方程的根决定,所以再对其对应的判别式分三种情况讨论求得对应解集即可.
解答:解:(1)若f(0)≥1,则-a|a|≥1?
?a≤-1
(2)当x≥a时,f(x)=3x2-2ax+a2,∴f(x)min=
=
,
如图所示:
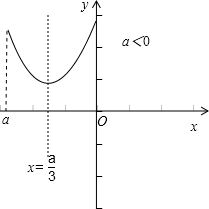
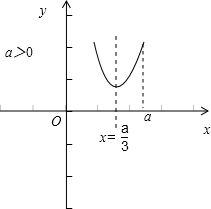
当x≤a时,f(x)=x2+2ax-a2,
∴f(x)min=
=
.
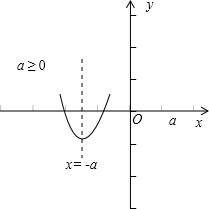
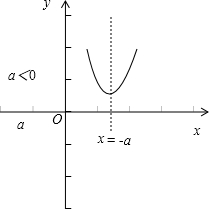
综上所述:f(x)min=
.
(3)x∈(a,+∞)时,h(x)≥1,
得3x2-2ax+a2-1≥0,△=4a2-12(a2-1)=12-8a2
当a≤-
或a≥
时,△≤0,x∈(a,+∞);
当-
<a<
时,△>0,得:
即
综上可得,
当a∈(-∞,-
)∪(
,+∞)时,不等式组的解集为(a,+∞);
当a∈(-
,-
)时,不等式组的解集为(a,
]∪[
,+∞);
当a∈[-
,
]时,不等式组的解集为[
,+∞).
|
(2)当x≥a时,f(x)=3x2-2ax+a2,∴f(x)min=
|
|
如图所示:


当x≤a时,f(x)=x2+2ax-a2,
∴f(x)min=
|
|


综上所述:f(x)min=
|
(3)x∈(a,+∞)时,h(x)≥1,
得3x2-2ax+a2-1≥0,△=4a2-12(a2-1)=12-8a2
当a≤-
| ||
| 2 |
| ||
| 2 |
当-
| ||
| 2 |
| ||
| 2 |
|
即
|
综上可得,
当a∈(-∞,-
| ||
| 2 |
| ||
| 2 |
当a∈(-
| ||
| 2 |
| ||
| 2 |
a-
| ||
| 3 |
a+
| ||
| 3 |
当a∈[-
| ||
| 2 |
| ||
| 2 |
a+
| ||
| 3 |
点评:本题考查了分段函数的最值问题.分段函数的最值的求法是先对每一段分别求最值,最后综合最大的为整个函数的最大值,最小的为整个函数的最小值.

练习册系列答案
相关题目