题目内容
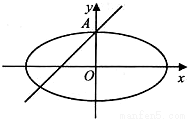
如图所示,椭圆![]() 的离心率为
的离心率为![]() ,且A(0,1)是椭圆C的顶点.
,且A(0,1)是椭圆C的顶点.
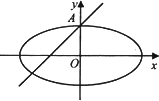
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线l,设以椭圆C的右焦点F为抛物线E:y2=2px(p>0)的焦点,若点M为抛物线E上任意一点,求点M到直线l距离的最小值.
答案:
解析:
解析:
解:(1)由题意可知,![]() 1分
1分
![]()
即![]() 3分
3分
![]() 所以椭圆C的方程为:
所以椭圆C的方程为:![]() 4分
4分
(2)方法一:由(1)可求得椭圆C的右焦点坐标F(1,0) 6分
![]() 抛物线E的方程为:
抛物线E的方程为:![]() ,
,
而直线![]() 的方程为
的方程为![]()
设动点M为![]() ,则点M到直线
,则点M到直线![]() 的距离为 8分
的距离为 8分
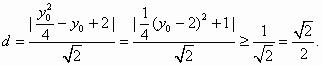 13分
13分
即抛物线E上的点到直线![]() 距离的最小值为
距离的最小值为![]() 14分
14分
方法二:由(1)可求得椭圆C的右焦点坐标F(1,0) 6分
![]() 抛物线E的方程为:
抛物线E的方程为:![]() ,
,
而直线![]() 的方程为
的方程为![]()
可设与直线![]() 平行且抛物线E相切的直线
平行且抛物线E相切的直线![]() 方程为:
方程为:![]() 8分
8分
由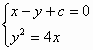
可得:![]() 9分
9分
![]() ,
,
解得:![]() ,
,
![]() 直线
直线![]() 方程为:
方程为:![]() 11分
11分
![]() 抛物线上的点到直线的距离的最小值等于直线
抛物线上的点到直线的距离的最小值等于直线![]() 与
与![]() 的距离:
的距离:
![]() 13分
13分
即抛物线E上的点到直线![]() 距离的最小值为
距离的最小值为![]() 14分
14分


练习册系列答案
相关题目
 的离心率为
的离心率为 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
 ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线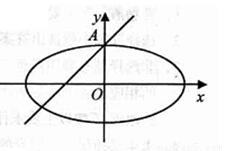
 的离心率为
的离心率为 ,且A(0,2)是椭圆C的顶点.
,且A(0,2)是椭圆C的顶点.
 的离心率为
的离心率为 ,且A(0,1)是椭圆C的顶点.
,且A(0,1)是椭圆C的顶点.
 的离心率为
的离心率为 ,且A(0,1)是椭圆C的顶点.
,且A(0,1)是椭圆C的顶点.
 的离心率为
的离心率为 ,且A(0,2)是椭圆C的顶点.
,且A(0,2)是椭圆C的顶点.