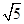题目内容
已知边长为1的正方形ABCD，则|
+
+
|=
| AB |
| BC |
| CD |
1
1
．分析：作出正方形ABCD，根据向量加法的几何意义可得
+
=
，从而
+
+
=
，从而得出
+
+
的模长，问题解决
| AB |
| BC |
| AC |
| AB |
| BC |
| CD |
| AD |
| AB |
| BC |
| CD |
解答：解：利用向量加法的几何性质，得
+
=
∴
+
+
=
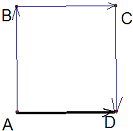
因为正方形的边长等于1
所以|
+
+
|=|
| =1
故答案为：1
| AB |
| BC |
| AC |
∴
| AB |
| BC |
| CD |
| AD |
因为正方形的边长等于1
所以|
| AB |
| BC |
| CD |
| AD |
故答案为：1
点评：本题考查两个向量的加、减法的法则，以及其几何意义，向量的模的定义．根据题意画出图形，利用图形结合正方形的性质解题，是解决本题的关键．
练习册系列答案
相关题目
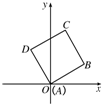已知边长为1的正方形ABCD中，AB与x轴正半轴成30°角．求点B和点D的坐标和
，则直线BC与平面ABD所成角的正弦值为（ ）
B.
C.
D.
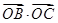的最大值是（
）
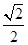C．2 D．