题目内容
.设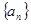 是公比为
是公比为 的等比数列,
的等比数列,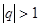 ,令
,令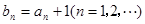 ,若数列
,若数列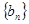 有连续四项在集合
有连续四项在集合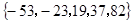 中,则
中,则 ★ .
★ .
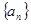 是公比为
是公比为 的等比数列,
的等比数列,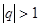 ,令
,令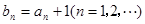 ,若数列
,若数列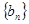 有连续四项在集合
有连续四项在集合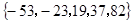 中,则
中,则 ★ .
★ .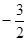
分析:根据bn=an+1可知 an=bn-1,依据{bn}有连续四项在{-53,-23,19,37,82}中,则可推知则{an}有连续四项在{-54,-24,18,36,81}中,按绝对值的顺序排列上述数值,可求{an}中连续的四项,求得q
解:{bn}有连续四项在{-53,-23,19,37,82}中且bn=an+1 an=bn-1
则{an}有连续四项在{-54,-24,18,36,81}中
∵{an}是等比数列,等比数列中有负数项则q<0,且负数项为相隔两项
∴等比数列各项的绝对值递增或递减,按绝对值的顺序排列上述数值18,-24,36,-54,81}
相邻两项相除-
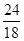 =-
=-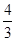 ,-
,-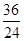 =-
=-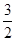 ,-
,-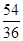 =-
=-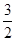 ,
,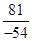 =-
=-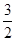
则可得,-24,36,-54,81是{an}中连续的四项,此时q=-
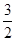

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且
 ,
, 及
及 ;(2)证明:数列
;(2)证明:数列 .
.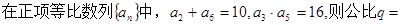 ( )
( )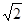
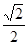

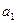 ,
, ,…,
,…,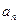 ,
,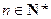 ,
,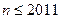 .(注:框图中的赋值符号“
.(注:框图中的赋值符号“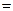 ”也可以写成“
”也可以写成“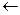 ”或“:
”或“: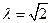 ,写出输出结果;
,写出输出结果;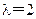 ,令
,令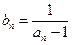 ,证明
,证明 是等差数列,并写出数列
是等差数列,并写出数列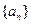 的通项公式;
的通项公式;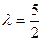 ,令
,令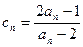 ,
,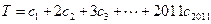 .
.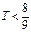 .
.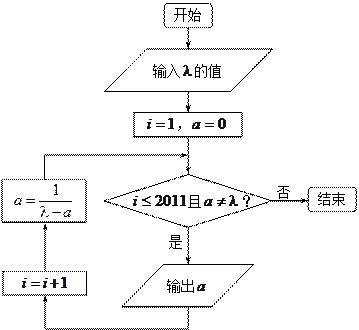
 中,
中,
 为等比数列;
为等比数列; 项的和为
项的和为 ,若
,若 ,求:正
,求:正 整数
整数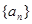 中,如果
中,如果
 为 ( )
为 ( )

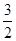

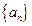 满足
满足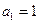 ,
,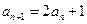 ,若数列
,若数列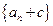 恰为等比数列,则
恰为等比数列,则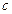 的值为 .
的值为 .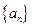 中,
中,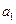 和
和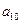 是方程
是方程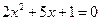 的两个根,则
的两个根,则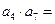 ( )
( )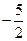

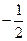
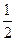
 中,
中, ,则
,则 等于
等于