题目内容
设 ,函数
,函数 的最大值为1,最小值为
的最大值为1,最小值为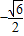 ,求常数a,b.
,求常数a,b.
【答案】分析:这是一道求函数的最值的逆向思维问题.本题的关键是比较极值和端点处的函数值的大小,列表解题一目了然,从而确定出a,b的值.
解答:解:f′(x)=3x(x-a)当x变化时,列表如下:
当x=0时,f(x)取极大值b,而f(0)>f(a),f(-1)<f(1),故需比较f(0)与f(1)的大小.
∵ ,∴f(x)最大值为f(0)=b=1.
,∴f(x)最大值为f(0)=b=1.
又 ,∴f(x)min=f(-1),∴
,∴f(x)min=f(-1),∴ ,
,
综上知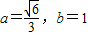
点评:导数的涉入,为解决函数问题提供了一般性的方法及简捷地解决一些实际问题,参数的取值(范围)问题一直是全面考查学生数学素养的一类好题.利用导数,结合单调区间,借助于函数的最值是解决这类问题的最常见的方法.
解答:解:f′(x)=3x(x-a)当x变化时,列表如下:
| x | -1 | (-1,0) | (0,a) | a | (a,1) | 1 | |
| f′(x) | + | - | + | ||||
| f(x) |  | b |  |  |
∵
 ,∴f(x)最大值为f(0)=b=1.
,∴f(x)最大值为f(0)=b=1.又
 ,∴f(x)min=f(-1),∴
,∴f(x)min=f(-1),∴ ,
,综上知
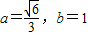
点评:导数的涉入,为解决函数问题提供了一般性的方法及简捷地解决一些实际问题,参数的取值(范围)问题一直是全面考查学生数学素养的一类好题.利用导数,结合单调区间,借助于函数的最值是解决这类问题的最常见的方法.

练习册系列答案
相关题目
 满足约束条件.
满足约束条件. 若目标函数
若目标函数 的最大值为1,则
的最大值为1,则 的最小值为
.
的最小值为
. ,函数
,函数 的最大值为1,最小值为
的最大值为1,最小值为 ,常数
,常数 的值是_____________.
的值是_____________. ,函数
,函数 的最大值为1,最小值为
的最大值为1,最小值为 ,则常数
,则常数 的值分别为
和
的值分别为
和
 ,函数
,函数 的最大值为1,
的最大值为1, ,则常数
,则常数 的值分别为 和
的值分别为 和