题目内容
在平等四边形ABCD中,已知AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P在BC(包括端点),则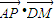 的取值范围是 .
的取值范围是 .
【答案】分析:先设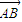 =
=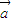 ,
,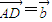 ,则|
,则|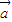 |=2,|
|=2,|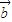 |=1,
|=1,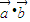 =1,然后计算点P在BC上时
=1,然后计算点P在BC上时 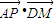 的取值范围,从而求出所求.
的取值范围,从而求出所求.
解答:解:设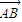 =
=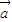 ,
,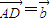 ,则|
,则|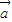 |=2,|
|=2,|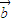 |=1,
|=1,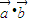 =1,
=1,
当点P在BC上时,设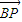 =λ
=λ 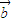 ,λ∈[0,1]
,λ∈[0,1]
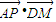 =(
=(  λ
λ 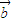 )(
)(
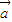 -
-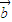 )=2-λ+
)=2-λ+ λ-1=1-
λ-1=1- λ∈[
λ∈[ ,1]
,1]
故答案为:[ ,1].
,1].
点评:本题主要考查了平面向量数量积的运算,以及共线向量的表示,属于中档题.
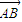 =
=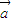 ,
,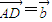 ,则|
,则|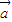 |=2,|
|=2,|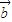 |=1,
|=1,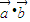 =1,然后计算点P在BC上时
=1,然后计算点P在BC上时 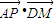 的取值范围,从而求出所求.
的取值范围,从而求出所求.解答:解:设
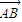 =
=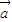 ,
,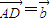 ,则|
,则|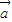 |=2,|
|=2,|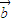 |=1,
|=1,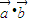 =1,
=1,当点P在BC上时,设
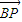 =λ
=λ 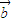 ,λ∈[0,1]
,λ∈[0,1]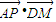 =(
=(  λ
λ 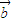 )(
)(
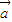 -
-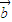 )=2-λ+
)=2-λ+ λ-1=1-
λ-1=1- λ∈[
λ∈[ ,1]
,1]故答案为:[
 ,1].
,1].点评:本题主要考查了平面向量数量积的运算,以及共线向量的表示,属于中档题.

练习册系列答案
相关题目
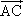 =a,
=a,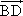 =b,则
=b,则 =
=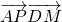 的取值范围是________.
的取值范围是________.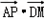 的取值范围是( )
的取值范围是( )