题目内容
【题目】在光滑的水平地面上有一辆车,车内有一个人和N个铅球,系统原来处于静止状态。现车内的人以一定的水平速度将铅球一个一个地向车外抛出,车子和人将获得反冲速度。第一过程,保持每次相对地面抛球速率均为v,直到将球抛完;第二过程,保持每次相对车子抛球速率均为v,直到将球抛完。试问:哪一过程使车子获得的速度更大?
【答案】第一过程使车子获得的速度较大。
【解析】
动量守恒定律必须选取研究对象之外的第三方为参照,这意味着,本问题中不能选车子为参照。一般选地面为参考系,这样对“第二过程”的铅球动量表达,就形成了难点,必须引进相对速度与绝对速度的关系。至于“第一过程”,比较简单:N次抛球和将N个球一次性抛出是完全等效的。
设车和人的质量为M,每个铅球的质量为m。由于矢量的方向落在一条直线上,可以假定一个正方向后,将矢量运算化为代数运算。设车速方向为正,且第一过程获得的速度大小为![]() ,第二过程获得的速度大小为
,第二过程获得的速度大小为![]() 。
。
第一过程,由于铅球每次的动量都相同,可将多次抛球看成一次抛出。
由车子、人和N个球动量守恒有
![]() ,得
,得![]() 。 ①
。 ①
第二过程,必须逐次考查铅球与车子(人)的作用。
第一个球与(N-1)个球、人、车系统作用,完毕后,设“系统”速度为![]() 。值得注意的是,根据运动合成法则,
。值得注意的是,根据运动合成法则,![]() ,铅球对地的速度并不是
,铅球对地的速度并不是![]() ,而是
,而是![]() 。它们的动量守恒方程为
。它们的动量守恒方程为
![]() ,
,
得![]() 。
。
第二个球与(N-2)个球、人、车系统作用,完毕后,设“系统”速度为![]() 。它们动量守恒方程为
。它们动量守恒方程为
![]()
![]() ,
,
得![]() 。
。
第三个球与(N-3)个球、人、车系统作用,完毕后,设“系统”速度为![]() 。铅球对地的速度是
。铅球对地的速度是![]() 。它们动量守恒方程为
。它们动量守恒方程为
![]()
![]() ,
,
得![]() 。
。
以此类推(过程注意:先找![]() 和
和![]() 关系,再看
关系,再看![]() 和v的关系,不要急于化简通分),
和v的关系,不要急于化简通分),![]() 的通式已经可以找出:
的通式已经可以找出:
![]()
![]() 。
。
不难发现,![]() 和
和![]() 都有N项,每项的分子都相同,但
都有N项,每项的分子都相同,但![]() 式中每项的分母都比②式中的分母小,所以
式中每项的分母都比②式中的分母小,所以![]() 。结论:第一过程使车子获得的速度较大。
。结论:第一过程使车子获得的速度较大。
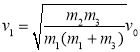
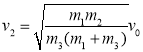

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案