题目内容
 如图所示,轻质杠杆OA中点悬挂重为100N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是
如图所示,轻质杠杆OA中点悬挂重为100N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是50N
50N
,保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将不变
不变
(选填“变大”、“变小”、或“不变”,下同).若本实验中F的方向始终与棒垂直,则F将变小
变小
.分析:(1)在A位置如图,OA、OC为动力F和阻力G的力臂,知道C是OA的中点,也就知道两力臂的大小关系,知道阻力G的大小,利用杠杆的平衡条件求动力F的大小;
(2)在B位置,画出动力和阻力的作用线,找出动力臂的阻力臂,利用三角形的相似关系,确定动力臂和阻力臂的大小关系,再利用杠杆平衡条件分析拉力F的大小变化情况;
(3)根据力臂变化情况,应用杠杆平衡条件分析答题.
(2)在B位置,画出动力和阻力的作用线,找出动力臂的阻力臂,利用三角形的相似关系,确定动力臂和阻力臂的大小关系,再利用杠杆平衡条件分析拉力F的大小变化情况;
(3)根据力臂变化情况,应用杠杆平衡条件分析答题.
解答: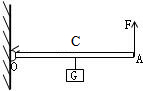 解:(1)如图,杠杆在A位置,LOA=2LOC,
解:(1)如图,杠杆在A位置,LOA=2LOC,
∵杠杆平衡,
∴FLOA=GLOC,
∴F=
=
G=
×100N=50N;
(2)杠杆在B位置,OA′为动力臂,OC′为阻力臂,阻力不变为G,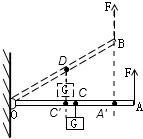
∵△OC′D∽△OA′B,
∴OC′:OA′=OD:OB=1:2,
∵杠杆平衡,
∴F′LOA′=GLOC′,
∴F′=
=
G=
×100N=50N;由此可知当杠杆从A位置匀速提到B位置的过程中,力F的大小不变;
(3)将杠杆从A位置匀速提升到B位置的过程中,如果F的方向始终与棒垂直,则力F的力臂不变,阻力G不变,阻力臂变小,
由杠杆平衡条件可得,动力F将变小.
故答案为:50N;不变;变小.
 解:(1)如图,杠杆在A位置,LOA=2LOC,
解:(1)如图,杠杆在A位置,LOA=2LOC,∵杠杆平衡,
∴FLOA=GLOC,
∴F=
| GLOC |
| LOA |
| 1 |
| 2 |
| 1 |
| 2 |
(2)杠杆在B位置,OA′为动力臂,OC′为阻力臂,阻力不变为G,

∵△OC′D∽△OA′B,
∴OC′:OA′=OD:OB=1:2,
∵杠杆平衡,
∴F′LOA′=GLOC′,
∴F′=
| G×LOC′ |
| LOA′ |
| 1 |
| 2 |
| 1 |
| 2 |
(3)将杠杆从A位置匀速提升到B位置的过程中,如果F的方向始终与棒垂直,则力F的力臂不变,阻力G不变,阻力臂变小,
由杠杆平衡条件可得,动力F将变小.
故答案为:50N;不变;变小.
点评:本题考查了学生对杠杆平衡条件的了解和掌握,能画出杠杆在B位置的力臂并借助三角形相似确定其关系是本题的关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 21、如图所示,轻质杠杆可绕O转动,杠杆上吊一重物G,在力F作用下杠杆静止在水平位置,l为F的力臂,请在图中作出力F的示意图及重物G所受重力的示意图.
21、如图所示,轻质杠杆可绕O转动,杠杆上吊一重物G,在力F作用下杠杆静止在水平位置,l为F的力臂,请在图中作出力F的示意图及重物G所受重力的示意图.
 (2011?金山区二模)如图所示,轻质杠杆OB可绕O点转动,OA的长0.3米,AB的长0.1米,B点处挂一个质量为3千克的物体M,A点处加一个竖直向上的力F,杠杆在水平位置平衡,则物体M的重力大小为
(2011?金山区二模)如图所示,轻质杠杆OB可绕O点转动,OA的长0.3米,AB的长0.1米,B点处挂一个质量为3千克的物体M,A点处加一个竖直向上的力F,杠杆在水平位置平衡,则物体M的重力大小为 如图所示,轻质杠杆OA可绕O点转动,杠杆长0.2米,在它的中点B处挂一重30牛的物体G.若在杠杆上A端施加最小的力F,使杠杆在水平位置平衡,画力F的方向并求出力F大小为多少牛?
如图所示,轻质杠杆OA可绕O点转动,杠杆长0.2米,在它的中点B处挂一重30牛的物体G.若在杠杆上A端施加最小的力F,使杠杆在水平位置平衡,画力F的方向并求出力F大小为多少牛?