题目内容
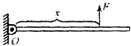 如图,长3.0m、重10N且密度不均匀的金属杆,可绕O点在竖直平面内自由转动.现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如表.
如图,长3.0m、重10N且密度不均匀的金属杆,可绕O点在竖直平面内自由转动.现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如表.| 试验次数 | x/m | P/N |
| 1 | 0.5 | 20 |
| 2 | 1.0 | 10 |
| 3 | 1.5 | 6.7 |
| 4 | 2.0 | 5 |
| 5 | 2.5 | 4 |
F=
| 10N?m |
| x |
F=
.| 10N?m |
| x |
(2)O点到金属杆重心的距离为
1
1
m.(3)若测力计量程为25N,则x控制在
0.4m≤x≤3.0m
0.4m≤x≤3.0m
范围.分析:(1)根据表中数据分析距离与拉力的关系,然后找出F与x间的关系.
(2)根据杠杆平衡的条件:动力×动力臂=阻力×阻力臂,根据表中数据列平衡方程,然后解方程求出金属杆的位置.
(3)当动力等于25N时,根据杠杆平衡条件:动力×动力臂=阻力×阻力臂,求出动力臂,这是最小动力臂.
(2)根据杠杆平衡的条件:动力×动力臂=阻力×阻力臂,根据表中数据列平衡方程,然后解方程求出金属杆的位置.
(3)当动力等于25N时,根据杠杆平衡条件:动力×动力臂=阻力×阻力臂,求出动力臂,这是最小动力臂.
解答:解:(1)从表中数据可以看出,当动力臂x增大时,拉力F逐渐减小,
并且Fx是一个定值,且Fx=20N×0.5m=10N?m,则F与x之间的关系是F=
.
故答案为:F=
.
(2)设O点到金属杆重心的距离为L,即重力的力臂为L,
由表中数据知:F=20N,x=0.5m,由杠杆平衡的条件:动力×动力臂=阻力×阻力臂,
得:G×L=F×x,O点到金属杆重心的距离L=
=
=1m.
故答案为:1.
(3)当拉力等于测力计量程F=25N时,拉力最大,拉力的力臂最小,
由杠杆平衡的条件:动力×动力臂=阻力×阻力臂,
得:G×L=F最大×x最小,x最小=
=
=0.4m;
拉力力臂的最大值是金属杆的长度L最大=3m;
则x范围是:0.4m≤x≤3m.
故答案为:0.4m≤x≤3m.
并且Fx是一个定值,且Fx=20N×0.5m=10N?m,则F与x之间的关系是F=
| 10N?m |
| x |
故答案为:F=
| 10N?m |
| x |
(2)设O点到金属杆重心的距离为L,即重力的力臂为L,
由表中数据知:F=20N,x=0.5m,由杠杆平衡的条件:动力×动力臂=阻力×阻力臂,
得:G×L=F×x,O点到金属杆重心的距离L=
| F×x |
| G |
| 20N×0.5m |
| 10N |
故答案为:1.
(3)当拉力等于测力计量程F=25N时,拉力最大,拉力的力臂最小,
由杠杆平衡的条件:动力×动力臂=阻力×阻力臂,
得:G×L=F最大×x最小,x最小=
| G×L |
| F最大 |
| 10N×1m |
| 25N |
拉力力臂的最大值是金属杆的长度L最大=3m;
则x范围是:0.4m≤x≤3m.
故答案为:0.4m≤x≤3m.
点评:本题考查了杠杆平衡条件的应用,解决与杠杆平衡条件相关问题的基本方法:准确找出支点、动力与动力臂、阻力与阻力臂,然后由平衡条件列方程求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
(3分)如图,长3.0m、重10N且密度不均匀的金属杆,可绕O点在竖直平面内自由转动。现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如右表。
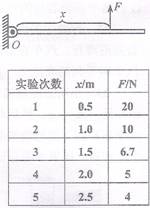 |
(1)由表中数据可得F与x之间的关系是:
(2)O点到金属杆重心的距离为 m。
(3)若测力计量程为25N,则应控制在 范围。
(3分)如图,长3.0m、重10N且密度不均匀的金属杆,可绕O点在竖直平面内自由转动。现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如右表。
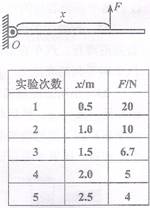 |
(1)由表中数据可得F与x之间的关系是:
(2)O点到金属杆重心的距离为 m。
(3)若测力计量程为25N,则应控制在 范围。
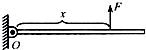 30、如图,长3.0m、重10N且密度不均匀的金属杆,可绕O点在竖直平面内自由转动.现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如下表.
30、如图,长3.0m、重10N且密度不均匀的金属杆,可绕O点在竖直平面内自由转动.现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如下表.
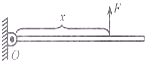 如图,长3.0m、重10N且密度不均匀的金属杆,绕O点在竖直平面内自由转动.现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如表.
如图,长3.0m、重10N且密度不均匀的金属杆,绕O点在竖直平面内自由转动.现用竖直向上的拉力F使金属杆保持水平,测出O点到拉力F的距离及F的大小,再改变拉力F作用点的位置,测出相应的F与x的大小,所得实验数据如表.