题目内容
A:某小组研究“杠杆平衡条件”,

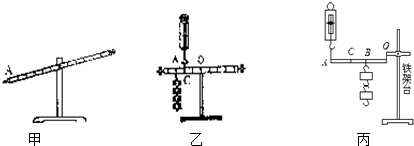
(1)当杠杆静止在如图甲所示位置时,处于
(2)实验中改变钩码位置和个数,一般要做三次,其目的是
(3)如图乙所示,弹簧测力计在C处由竖直向上逐渐向右倾斜拉动杠杆,仍使杠杆在水平位置保持平衡,则弹簧测力计的示数将
B:如图丙所示为研究“杠杆机械效率”的装置,每个钩码重为G,O为支点.
(1)将2只钩码挂在B点,在A点竖直向上匀速拉动弹簧测力计,拉力为F1,测得A、B两点上升的高度分别为h1、h2,则杠杆的机械效率为η=
×100%
×100%.(用物理量的符号表示)
(2)将2只钩码挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度为h2,则弹簧测力计的示数将
(3)将3只钩码挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度仍为h2,则与前两次相比,第三次杠杆的机械效率

(1)当杠杆静止在如图甲所示位置时,处于
平衡
平衡
(“平衡”或“不平衡”)状态.此时调节两端的平衡螺母,使杠杆在水平位置平衡,这样做是为了便于测量力臂,同时消除杠杆自身重对杠杆平衡的影响
便于测量力臂,同时消除杠杆自身重对杠杆平衡的影响
.(2)实验中改变钩码位置和个数,一般要做三次,其目的是
得到的结论具有普遍性
得到的结论具有普遍性
.(3)如图乙所示,弹簧测力计在C处由竖直向上逐渐向右倾斜拉动杠杆,仍使杠杆在水平位置保持平衡,则弹簧测力计的示数将
变大
变大
(选填“变大”、“变小”或“保持不变”),其原因是其力臂减小
其力臂减小
.B:如图丙所示为研究“杠杆机械效率”的装置,每个钩码重为G,O为支点.
(1)将2只钩码挂在B点,在A点竖直向上匀速拉动弹簧测力计,拉力为F1,测得A、B两点上升的高度分别为h1、h2,则杠杆的机械效率为η=
| 2mgh2 |
| F1h1 |
| 2mgh2 |
| F1h1 |
(2)将2只钩码挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度为h2,则弹簧测力计的示数将
大于
大于
(大于/等于/小于)F1.(3)将3只钩码挂在C点,在A点竖直向上匀速拉动弹簧测力计,使C点上升高度仍为h2,则与前两次相比,第三次杠杆的机械效率
最大
最大
(最大/最小/三次相等).分析:(1)杠杆处于静止状态或匀速转动状态时,杠杆处于平衡状态;使杠杆在水平位置平衡,这是为了便于测量力臂,同时使杠杆所受的重力通过支点,从而可以不考虑杠杆自身的重力对其转动的影响;
(2)实验规律应建立在多次测量的基础上,以避免得到偶然性的结论;
(3)根据杠杆平衡条件F1L1=F2L2进行判断;
(4)使用杠杆克服钩码的重力做功,有用功等于克服钩码重力做的功,总功等于弹簧测力计的拉力做的功,机械效率等于有用功和总功的比值;
(5)从图中可以看出,将2只钩码悬挂在C点时,重力的力臂大于在B点重力的力臂,而动力臂不变,根据杠杆平衡的条件可知弹簧测力计的示数的变化情况;
(6)分析有用功、额外功的变化,然后根据机械效率公式即可得出正确结果.
(2)实验规律应建立在多次测量的基础上,以避免得到偶然性的结论;
(3)根据杠杆平衡条件F1L1=F2L2进行判断;
(4)使用杠杆克服钩码的重力做功,有用功等于克服钩码重力做的功,总功等于弹簧测力计的拉力做的功,机械效率等于有用功和总功的比值;
(5)从图中可以看出,将2只钩码悬挂在C点时,重力的力臂大于在B点重力的力臂,而动力臂不变,根据杠杆平衡的条件可知弹簧测力计的示数的变化情况;
(6)分析有用功、额外功的变化,然后根据机械效率公式即可得出正确结果.
解答:解:A:(1)杠杆静止在如图甲所示位置,杠杆处于静止状态,所以此时杠杆处于平衡状态;调节杠杆在水平位置平衡,目的是便于从杠杆上测量力臂,同时是为了让杠杆的重心在支点上,可避免杠杆自重的影响;
(2)在多次实验的基础上通过分析才能得出结论,排除偶然性,得到普遍的规律.
(3)杠杆在水平位置平衡,阻力、阻力臂不变,弹簧测力计倾斜拉动杠杆时,动力臂变小,动力变大,所以弹簧测力计示数会变大;
B:(1)有用功为W有=Gh2=2mgh2,总功W总=F1h1,则机械效率的表达式η=
×100%=
×100%;
(2)钩码的悬挂点在B点时,由杠杠的平衡条件得F1?OA=G?OB;悬挂点移至C点时,由杠杠的平衡条件得F2?OA=G?OC;从图中可以看出,由OB到OC,力臂变大,所以弹簧测力计的示数变大;
(3)因为第一次与第二次的有用功相等,并且第二次的额外功小,因为机械效率等于有用功与总功的比值,因此第一次的机械效率小于第二次的机械效率;
将3只钩码悬挂在C点时,物体升高的高度不变,物重增加,由W有=Gh2可得,有用功变大,但杠杆提升的高度与第二次相同,额外功与第二次相同,又因为机械效率等于有用功与总功的比值,因此第三次的机械效率大于第二次的机械效率.
综上所述,第三次的机械效率最大.
故答案为:A:(1)平衡;便于测量力臂,同时消除杠杆自身重对杠杆平衡的影响;(2)得到的结论具有普遍性;(3)变大;其力臂减小;
B:(1)
×100%;(2)大于;(3)最大.
(2)在多次实验的基础上通过分析才能得出结论,排除偶然性,得到普遍的规律.
(3)杠杆在水平位置平衡,阻力、阻力臂不变,弹簧测力计倾斜拉动杠杆时,动力臂变小,动力变大,所以弹簧测力计示数会变大;
B:(1)有用功为W有=Gh2=2mgh2,总功W总=F1h1,则机械效率的表达式η=
| W有用 |
| W总 |
| 2mgh2 |
| F1h1 |
(2)钩码的悬挂点在B点时,由杠杠的平衡条件得F1?OA=G?OB;悬挂点移至C点时,由杠杠的平衡条件得F2?OA=G?OC;从图中可以看出,由OB到OC,力臂变大,所以弹簧测力计的示数变大;
(3)因为第一次与第二次的有用功相等,并且第二次的额外功小,因为机械效率等于有用功与总功的比值,因此第一次的机械效率小于第二次的机械效率;
将3只钩码悬挂在C点时,物体升高的高度不变,物重增加,由W有=Gh2可得,有用功变大,但杠杆提升的高度与第二次相同,额外功与第二次相同,又因为机械效率等于有用功与总功的比值,因此第三次的机械效率大于第二次的机械效率.
综上所述,第三次的机械效率最大.
故答案为:A:(1)平衡;便于测量力臂,同时消除杠杆自身重对杠杆平衡的影响;(2)得到的结论具有普遍性;(3)变大;其力臂减小;
B:(1)
| 2mgh2 |
| F1h1 |
点评:(1)杠杆平衡条件应用比较广泛,利用杠杆平衡条件可以判断杠杆是否平衡、力臂大小、力的大小等.
(2)本题考查杠杆机械效率的测量,把握有用功、总功的计算方式,明确机械效率的表达式,知道总功等于有用功与额外功之和.
(2)本题考查杠杆机械效率的测量,把握有用功、总功的计算方式,明确机械效率的表达式,知道总功等于有用功与额外功之和.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
如图1所示,某小组研究“杠杆的平衡条件”,器材:有刻度的杠杆、若干个相同的钩码、弹簧测力计等,O为杠杆的支点.
①实验前,应先调节杠杆在 位置平衡.这样做,除了可以消除自身的重力影响,还可以方便地测量或读出 .调节时,如发现杠杆左端偏高,应如何操作: .

②某实验小组记录两组数据如下:
根据分析,这组数据中,实验序号为 选填:“1”或“2”)的一组肯定有错误.检查发现是测量动力臂时读错了,动力臂的实际值比记录值 (选填:大或小).
③如图2所示,弹簧测力计在C处由竖直向上逐渐向右倾斜拉动杠杆,仍使杠杆在水平位置保持平衡,则弹簧测力计的示数将 (选填:变大、变小或保持不变),其原因是 .
④某次实验中,若采取如图3所示的方式悬挂钩码,杠杆也能在水平位置保持平衡(杠杆上每格等距),但老师却往往提醒大家不要采用这种方式,这主要是以下哪种原因 (选填字母).
A.一个人无法独立操作 B.需要使用太多的钩码
C.力臂与杠杆不重合 D.力和力臂数目过多
⑤如图4所示,实验小组选用长1.6m、粗细均匀的一只金属杆,绕O点在竖直平面内自由转动,同时将一个“拉力--位移传感器”竖直作用在杆上,并使杠杆在水平位置始终保持平衡.该传感器显示其拉力F与作用点到O点距离x的变化关系如图所示.由图5可知金属杆重 N.
①实验前,应先调节杠杆在

②某实验小组记录两组数据如下:
| 实验序号 | 动力F1/N | 动力臂L1/cm | 阻力F2/N | 阻力臂L2/cm |
| 1 | 2 | 20 | 1 | 10 |
| 2 | 1 | 8 | 2 | 4 |
③如图2所示,弹簧测力计在C处由竖直向上逐渐向右倾斜拉动杠杆,仍使杠杆在水平位置保持平衡,则弹簧测力计的示数将
④某次实验中,若采取如图3所示的方式悬挂钩码,杠杆也能在水平位置保持平衡(杠杆上每格等距),但老师却往往提醒大家不要采用这种方式,这主要是以下哪种原因
A.一个人无法独立操作 B.需要使用太多的钩码
C.力臂与杠杆不重合 D.力和力臂数目过多
⑤如图4所示,实验小组选用长1.6m、粗细均匀的一只金属杆,绕O点在竖直平面内自由转动,同时将一个“拉力--位移传感器”竖直作用在杆上,并使杠杆在水平位置始终保持平衡.该传感器显示其拉力F与作用点到O点距离x的变化关系如图所示.由图5可知金属杆重