Question

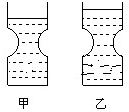如图所示，两个完全相同的杯子置于水平桌面上，甲装密度为ρ₁的液体，乙装密度为ρ₂的液体，两杯子底部所受液体压强相等，甲杯中液体质量为M₁，乙杯中液体质量为M₂．当把小球A放在甲杯中时，有1/4体积露出液面，此时液体对容器底部的压强为P₁；当把小球B放在乙杯中时，小球全部浸在液体中，此时液体对容器底部的压强为P₂（两次液体均未溢出）．已知ρ₁：ρ₂=5：4，两球体积相等．则下列判断正确的是（　　）

A、M₁＞M₂  P₁=P₂

B、M₁＜M₂  P₁＜P₂

C、M₁=M₂ P₁＞P₂

D、M₁＜M₂  P₁＞P₂

Answer 1

分析：（1）根据两杯子底部所受液体压强相等，利用圆柱形的容器G=F=ps的特点先得出重力相等，然后减去由于杯子凹进去而应减少的液体重力即可比较得出；
（2）小球A放在甲杯中漂浮，小球B放在乙杯中时，小球全部浸在液体中，根据公式p=ρgh求出液体对容器底部的压强p₁和p₂，进而根据ρ₁：ρ₂=5：4分析判断其代数式大小．

解答：解：①根据题意可知，两杯子底部所受液体压强相等，即：p₁=p₂，若杯子为圆柱形，则根据G=F=ps可知，G₁′=G₂′，
而由于杯子是如图所示形状，则甲、乙装的液体重力为：G₁=G₁′-△G₁′，G₂=G₂′-△G₂′；
因△G₁′=ρ₁△V，△G₂′=ρ₂△V；（△V为杯子凹进去的部分体积）
∵ρ₁：ρ₂=5：4，即ρ₁＞ρ₂，
∴△G₁′＞△G₂′，
∴M₁＜M₂；
②当把小球A放在甲杯中时，有

1

4

体积露出液面，则液体对容器底部的压强p₁=ρ₁g（h₁+

3 4 V

S

），
当把小球B放在乙杯中时，小球全部浸在液体中，则液体对容器底部的压强p₂=ρ₂g（h₂+

V

S

），
∴p₁-p₂=ρ₁g（h₁+

3 4 V

S

）-ρ₂g（h₂+

V

S

）
=（ρ₁gh₁-ρ₂gh₂）+（ρ₁g

3V

4S

-ρ₂g

V

S

）
=（ρ₁gh₁-ρ₂gh₂）+（

3

4

ρ₁-ρ₂）g

V

S

∵两杯子底部所受液体压强相等，则有ρ₁gh₁=ρ₂gh₂；
∵ρ₁：ρ₂=5：4，
∴ρ₁=

5

4

ρ₂，
∴

3

4

ρ₁-ρ₂=

3

4

×

5

4

ρ₂-ρ₂=（

15

16

-1）ρ₂＜0，
∴p₁-p₂＜0，
即p₁＜p₂．
故选B．

点评：本题考查液体质量和压强的比较，注意在不能直接求解的情况下，可以间接找出共同量去比较．本题是一道难题．