题目内容
 如图所示,R1为定值电阻,R2为滑动变阻器,当滑动变阻器的滑片P从最左端向右滑动时,下列说法中可能正确的是( )
如图所示,R1为定值电阻,R2为滑动变阻器,当滑动变阻器的滑片P从最左端向右滑动时,下列说法中可能正确的是( )| A、R1消耗的电功率不变,R2消耗的电功率变大 | B、R1消耗的电功率变小,R2消耗的电功率变大 | C、R1消耗的电功率变小,R2消耗的电功率变小 | D、R1消耗的电功率变小,R2消耗的电功率先变大后变小 |
分析:先列出滑动变阻器功率的计算式,再推导,求出它的最大值,并解出最大值时R2与R1的关系.本题应用到二次函数求最值.
解答:解:
P2=I22R2(R2的电功率等于流过R2的电流的平方乘以R2的阻值)
=I2R2 (串联电路电流处处相等,用总电流I代替I2)
=(
)2R2(总电流用总电压除以总电阻来代替)
=
(将平方分配到分子和分母上)
=
(将分母的完全平方和改成完全平方差,再加上4R1R2)
=
(将分子分母同时除以R2)
总电压U和电阻R1是定值,
≥0
当
最小时,P2最大
而
最小时R1=R2
即R1=R2时,R2电功率最大.
因此,当滑动变阻器的滑片从最左端滑向最右端时:
电路总电阻逐渐变大,干路电流逐渐变小,由P=I2R可判断出R1消耗的功率变小;
而R2消耗的功率要分情况讨论:
①R2最大值不大于R1时,R2由0逐渐变大,R2消耗的电功率变大;
②R2最大值大于R1时,R2由0逐渐变大,R2消耗的电功率先变大后变小;
故选D.
P2=I22R2(R2的电功率等于流过R2的电流的平方乘以R2的阻值)
=I2R2 (串联电路电流处处相等,用总电流I代替I2)
=(
| U |
| R1+R2 |
=
| U2R2 |
| (R1+R2)2 |
=
| U2R2 |
| (R1-R2)2+4R1R2 |
=
| U2 | ||
|
总电压U和电阻R1是定值,
| (R1-R2)2 |
| R2 |
当
| (R1-R2)2 |
| R2 |
而
| (R1-R2)2 |
| R2 |
即R1=R2时,R2电功率最大.
因此,当滑动变阻器的滑片从最左端滑向最右端时:
电路总电阻逐渐变大,干路电流逐渐变小,由P=I2R可判断出R1消耗的功率变小;
而R2消耗的功率要分情况讨论:
①R2最大值不大于R1时,R2由0逐渐变大,R2消耗的电功率变大;
②R2最大值大于R1时,R2由0逐渐变大,R2消耗的电功率先变大后变小;
故选D.
点评:这是关于电功率和欧姆定律的综合计算,应用的数学技巧很强,此题仅供学习基础好的学生做训练用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,R1为定值电阻,R2为滑动变阻器,电源电压保持不变.闭合开关S,在滑动变阻器的滑片P从a端向b端滑动的过程中( )
如图所示,R1为定值电阻,R2为滑动变阻器,电源电压保持不变.闭合开关S,在滑动变阻器的滑片P从a端向b端滑动的过程中( )| A、电流表示数变大,电压表V1示数变小,V2示数变大 | B、电流表示数变大,电压表V1示数变大,V2示数变小 | C、电流表示数变小,电压表V1示数变小,V2示数变大 | D、电流表示数变小,电压表V1示数变大,V2示数变小 |
 16、如图所示,R1为定值电阻,R2为滑动变阻器,则以下说法中正确的是( )
16、如图所示,R1为定值电阻,R2为滑动变阻器,则以下说法中正确的是( ) (2012?天津)如图所示,R1为定值电阻,R2为滑动变阻器,电源电压恒定,闭合开关S,调节滑动变阻器滑片,R1、R2两端的电压U1、U2与电流I的变化关系图象如下选项所示,其中正确的是( )
(2012?天津)如图所示,R1为定值电阻,R2为滑动变阻器,电源电压恒定,闭合开关S,调节滑动变阻器滑片,R1、R2两端的电压U1、U2与电流I的变化关系图象如下选项所示,其中正确的是( )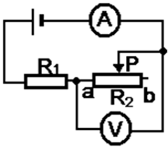 如图所示,R1为定值电阻,R2为滑动变阻器,电源电压U不变.当滑动变阻器的滑片P滑到a端和b端时,R1消耗的功率之比为9:1;且滑片P滑到a端时,电流表示数为6A,滑片P滑到b端时,电压表的示数为8V.求:电阻R1和R2阻值各为多少?电源电压多大?
如图所示,R1为定值电阻,R2为滑动变阻器,电源电压U不变.当滑动变阻器的滑片P滑到a端和b端时,R1消耗的功率之比为9:1;且滑片P滑到a端时,电流表示数为6A,滑片P滑到b端时,电压表的示数为8V.求:电阻R1和R2阻值各为多少?电源电压多大?