题目内容
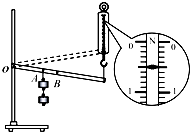 用如图所示的实验装置测量杠杆的机械效率.实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升.不考虑摩擦.
用如图所示的实验装置测量杠杆的机械效率.实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升.不考虑摩擦.(1)实验中,将两个相同的钩码悬挂在A点匀速将杠杆拉至图中虚线位置,测力计的示数F为
0.5
0.5
N,钩码总重G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率η1为66.7
66.7
%.(2)将三个相同的钩码悬挂在A点匀速提高时,该杠杆的机械效率为η2,则η2
>
>
η1.(</=/>)(3)将同一物体分别悬挂在A、B两点匀速提高时的机械效率分别为ηA和ηB,则ηA
<
<
ηB.(</=/>)分析:(1)对弹簧测力计进行读数时,需看清弹簧测力计的分度值,然后根据指针位置进行读数;在实验中,弹簧测力计向上拉力做的功是总功,克服钩码重力做的功是有用功,杠杆的机械效率可以根据公式η=
来计算.
(2)本实验中,不考虑摩擦时额外功是由克服杠杆自重做的功,将三个相同的钩码悬挂在A点匀速提高时,所做的额外功相同,根据有用功结合效率公式得出机械效率的变化.
(3)将同一物体分别悬挂在A、B两点时,改变了钩码重力的力臂,根据杠杆平衡条件分析,改变了弹簧测力计的拉力,改变了弹簧测力计的拉力做功的多少,改变了机械效率的高低.
| W有 |
| W总 |
(2)本实验中,不考虑摩擦时额外功是由克服杠杆自重做的功,将三个相同的钩码悬挂在A点匀速提高时,所做的额外功相同,根据有用功结合效率公式得出机械效率的变化.
(3)将同一物体分别悬挂在A、B两点时,改变了钩码重力的力臂,根据杠杆平衡条件分析,改变了弹簧测力计的拉力,改变了弹簧测力计的拉力做功的多少,改变了机械效率的高低.
解答:解:(1)由图可知,弹簧测力计的分度值是0.1N,所以它的示数是0.5N.
在实验过程中,有用功是:W有用=Gh=1N×0.1m=0.1J,
总功是:W总=Fs=0.5N×0.3m=0.15J,
所以杠杆的机械效率是:η=
=
≈66.7%.
(2)将三个相同的钩码悬挂在A点匀速提高时,所做的额外功相同,有用功增加,即有用功占总功的比值变大,所以此时的机械效率变大,即η2>η1.
(3)将同一物体由悬挂的A点变为B点时,物体的力臂变大,由杠杠的平衡条件可知拉力F变大;
杠杆提升的高度减小,额外功减小,因此有用功占总功的比值变大,即杠杆的机械效率变大.
故答案为:0.5;66.7%;>;<.
在实验过程中,有用功是:W有用=Gh=1N×0.1m=0.1J,
总功是:W总=Fs=0.5N×0.3m=0.15J,
所以杠杆的机械效率是:η=
| W有 |
| W总 |
| 0.1J |
| 0.15J |
(2)将三个相同的钩码悬挂在A点匀速提高时,所做的额外功相同,有用功增加,即有用功占总功的比值变大,所以此时的机械效率变大,即η2>η1.
(3)将同一物体由悬挂的A点变为B点时,物体的力臂变大,由杠杠的平衡条件可知拉力F变大;
杠杆提升的高度减小,额外功减小,因此有用功占总功的比值变大,即杠杆的机械效率变大.
故答案为:0.5;66.7%;>;<.
点评:本题考查杠杆机械效率的测量,把握有用功、总功的计算方式,明确机械效率的表达式和杠杆的平衡条件是关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
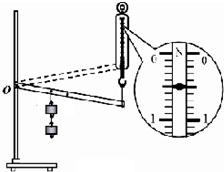 用如图所示的实验装置测量杠杆的机械效率.实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面钩码缓缓上升.实验中,将杠杆拉至图中虚线位置测力计的示数F=
用如图所示的实验装置测量杠杆的机械效率.实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面钩码缓缓上升.实验中,将杠杆拉至图中虚线位置测力计的示数F= (2005?云浮)用如图所示的实验装置测滑轮组的机械效率,实验中得到的一组数据列在下表中:
(2005?云浮)用如图所示的实验装置测滑轮组的机械效率,实验中得到的一组数据列在下表中: 用如图所示的实验装置测量斜面的机械效率.实验时,沿斜面向上匀速拉动弹簧测力计,使木块沿斜面匀速上升.为了研究斜面的机械效率与哪些因素有关,一位同学用该实验装置,先后用两木块做实验,测量并计算得到下表所示的两组数据:
用如图所示的实验装置测量斜面的机械效率.实验时,沿斜面向上匀速拉动弹簧测力计,使木块沿斜面匀速上升.为了研究斜面的机械效率与哪些因素有关,一位同学用该实验装置,先后用两木块做实验,测量并计算得到下表所示的两组数据: 小红同学用如图所示的实验装置测小车的平均速度.他用刻度尺测得斜面长为S=1.2m,小车通过前一半路程S1的时间为1s,通过全程S所用的时间是1.5s.那么,小车通过后一半路程S2的平均速度是
小红同学用如图所示的实验装置测小车的平均速度.他用刻度尺测得斜面长为S=1.2m,小车通过前一半路程S1的时间为1s,通过全程S所用的时间是1.5s.那么,小车通过后一半路程S2的平均速度是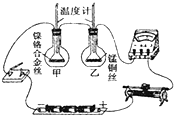 用如图所示的实验装置探究“电流通过导体产生的热量与电阻的关系”.
用如图所示的实验装置探究“电流通过导体产生的热量与电阻的关系”.