题目内容
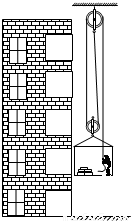
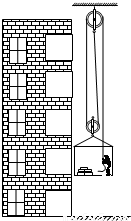
在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求:
(1)动滑轮的质量;
(2)此装置提升整块地板砖时的最高机械效率.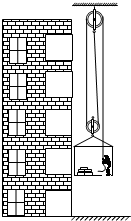
(1)动滑轮的质量;
(2)此装置提升整块地板砖时的最高机械效率.

(1)人的重力:
G人=m人g=85kg×10N/kg=850N,
提升8块地板砖时,地板砖的重力:
G砖1=8×100N=800N,
人对绳的拉力:
T1=
(G人+G砖1+G架+G动)=
(1750N+G动)
人对框架底的压力:
F1=G人-T1=850N-
(1750N+G动)
提升11块地板砖时,
地板砖的重力G砖2=11×100N=1100N
人对绳的拉力T2=
(G人+G砖2+G架+G动)=
(2050N+G动)
人对框架底的压力F2=G人-T2=850N-
(2050N+G动)
已知F1:F2=5:3
则,[850N-
(1750N+G动)]:[850N-
(2050N+G动)]=5:3
解得,动滑轮重G动=50N
动滑轮的质量m动=
=
=5kg,
(2)此装置的机械效率最高时,人对绳的拉力等于人的重力,即T=G人=850N,
地板砖、人、动滑轮和框架的总重应为G总=3T=2550N,
地板砖的最大重力G砖=G总-G人-G架-G动=2550N-850N-100N-50N=1550N.
因为题目要求提升整块砖,每块地板砖的重力为100N,
所以最多能提升地板砖的块数为:
=15.5块≈15块,
15块地板砖的重力G砖′=15×100N=1500N,
提升15块砖时,人对绳的实际拉力:
T′=
(G人+G砖′+G架+G动)=
(850N+1500N+100N+50N)=
,
设地板砖被提升的高度为h.
则,装置的最高机械效率η=
=
=
=60%.
答:(1)动滑轮的质量为5kg;
(2)此装置提升整块地板砖时的最高机械效率为60%.
G人=m人g=85kg×10N/kg=850N,
提升8块地板砖时,地板砖的重力:
G砖1=8×100N=800N,
人对绳的拉力:
T1=
| 1 |
| 3 |
| 1 |
| 3 |
人对框架底的压力:
F1=G人-T1=850N-
| 1 |
| 3 |
提升11块地板砖时,
地板砖的重力G砖2=11×100N=1100N
人对绳的拉力T2=
| 1 |
| 3 |
| 1 |
| 3 |
人对框架底的压力F2=G人-T2=850N-
| 1 |
| 3 |
已知F1:F2=5:3
则,[850N-
| 1 |
| 3 |
| 1 |
| 3 |
解得,动滑轮重G动=50N
动滑轮的质量m动=
| G动 |
| g |
| 50N |
| 10N/kg |
(2)此装置的机械效率最高时,人对绳的拉力等于人的重力,即T=G人=850N,
地板砖、人、动滑轮和框架的总重应为G总=3T=2550N,
地板砖的最大重力G砖=G总-G人-G架-G动=2550N-850N-100N-50N=1550N.
因为题目要求提升整块砖,每块地板砖的重力为100N,
所以最多能提升地板砖的块数为:
| 1550N |
| 100N |
15块地板砖的重力G砖′=15×100N=1500N,
提升15块砖时,人对绳的实际拉力:
T′=
| 1 |
| 3 |
| 1 |
| 3 |
| 2500N |
| 3 |
设地板砖被提升的高度为h.
则,装置的最高机械效率η=
| W有 |
| W总 |
| G′砖h |
| T′×3h |
| 1500N | ||
|
答:(1)动滑轮的质量为5kg;
(2)此装置提升整块地板砖时的最高机械效率为60%.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
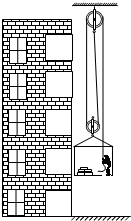 在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求:
在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求: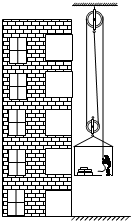 在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求:
在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求: