题目内容
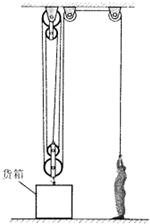 如图所示,质量为70kg的工人站在水平地面上,用带有货箱的滑轮组把货物运到高处.第一次运送货物时,放入货箱的货物质量为160kg,工人用力F1匀速拉绳的功率为P1,货箱以0.1m/s的速度匀速上升,地面对工人的支持力为N1.第二次运送货物时,放入货箱的货物质量为120kg,工人用力F2匀速拉绳,货箱以0.2m/s的速度匀速上升,地面对工人的支持力为N2,滑轮组机械效率为η2.N1与N2之比为15:19.(不计绳重及滑轮摩擦,g取10N/kg)
如图所示,质量为70kg的工人站在水平地面上,用带有货箱的滑轮组把货物运到高处.第一次运送货物时,放入货箱的货物质量为160kg,工人用力F1匀速拉绳的功率为P1,货箱以0.1m/s的速度匀速上升,地面对工人的支持力为N1.第二次运送货物时,放入货箱的货物质量为120kg,工人用力F2匀速拉绳,货箱以0.2m/s的速度匀速上升,地面对工人的支持力为N2,滑轮组机械效率为η2.N1与N2之比为15:19.(不计绳重及滑轮摩擦,g取10N/kg)求:(1)货箱和动滑轮的总质量m;
(2)功率P1;
(3)机械效率η2.
分析:(1)首先判断滑轮组的绳子段数为5,计算出人的重力和两次提升物体的重力,根据滑轮组特点计算出人拉绳子的拉力也就是绳子拉人的力,然后根据受力分析列出地面对人两次的支持力的表达式,把已知的值代入表达式计算出货箱和动滑轮的总质量;
(2)根据物体上升速度计算出拉力移动速度,根据第一问求的拉力,利用公式P=Fv计算拉力功率;
(3)利用第一问所求的动滑轮重力和第二次放入货箱的货物的重力,根据公式η=
来计算机械效率.
(2)根据物体上升速度计算出拉力移动速度,根据第一问求的拉力,利用公式P=Fv计算拉力功率;
(3)利用第一问所求的动滑轮重力和第二次放入货箱的货物的重力,根据公式η=
| G物 |
| G物+G动 |
解答: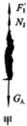
 解:(1)动滑轮和货箱总重为G.
解:(1)动滑轮和货箱总重为G.
第一次提升货物:
以人为研究对象,受力分析如图(甲)人所受的重力为:G人=m人g=70kg×10N/kg=700N;
运送的货物所受的重力为:G1=m1g=160kg×10N/kg=1600N;
绳对人的拉力F1′与人对绳的拉力F1大小相等:
F1′=
①
N1=G人-F1′②
第二次提升货物:以人为研究对象,受力分析如图4(乙)运送的货物所受的重为:
G2=m2g=120kg×10N/kg=1200N
绳对人的拉力F2′与人对绳的拉力F2大小相等:
F2′=
③
N2=G人-F2′④
=
⑤
把数据分别代入①②③④⑤解得:G=400N;F1′=400N.
m=
=
=40kg.
(2)第一次运送货物时,人匀速拉绳的力:F1=F1′=400N
货物匀速上升的速度:v1=0.1m/s;
人匀速拉绳的速度:v1′=5v1=5×0.1m/s=0.5m/s
P1=F1v1′=400N×0.5m/s=200W.
(3)第二次运送货物时滑轮组的机械效率:η2=
=
=
=
=75%.
答:(1)货箱和动滑轮的总质量m为40Kg;
(2)功率P1为200W;
(3)机械效率η2为75%.
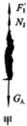
 解:(1)动滑轮和货箱总重为G.
解:(1)动滑轮和货箱总重为G.第一次提升货物:
以人为研究对象,受力分析如图(甲)人所受的重力为:G人=m人g=70kg×10N/kg=700N;
运送的货物所受的重力为:G1=m1g=160kg×10N/kg=1600N;
绳对人的拉力F1′与人对绳的拉力F1大小相等:
F1′=
| G1+G |
| 5 |
N1=G人-F1′②
第二次提升货物:以人为研究对象,受力分析如图4(乙)运送的货物所受的重为:
G2=m2g=120kg×10N/kg=1200N
绳对人的拉力F2′与人对绳的拉力F2大小相等:
F2′=
| G2+G |
| 5 |
N2=G人-F2′④
| N1 |
| N2 |
| 15 |
| 19 |
把数据分别代入①②③④⑤解得:G=400N;F1′=400N.
m=
| G |
| g |
| 400N |
| 10N/kg |
(2)第一次运送货物时,人匀速拉绳的力:F1=F1′=400N
货物匀速上升的速度:v1=0.1m/s;
人匀速拉绳的速度:v1′=5v1=5×0.1m/s=0.5m/s
P1=F1v1′=400N×0.5m/s=200W.
(3)第二次运送货物时滑轮组的机械效率:η2=
| W有 |
| W总 |
| G2h |
| (G2+G)h |
| G2 |
| G2+G |
| 1200N |
| 1200N+400N |
答:(1)货箱和动滑轮的总质量m为40Kg;
(2)功率P1为200W;
(3)机械效率η2为75%.
点评:这是综合性很强的题目,要用到重力、机械效率、速度以及滑轮的知识,所以是一道难题.另外,要学会用列方程的方法来解物理题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某小组三位同学发现钟摆的摆动似乎是有规律的.于是他们在细绳下面挂一小球制成了单摆,研究在摆动角度θ不大的情况下,单摆来回摆动一次所用的时间(摆动周期T)与哪些因素有关,如图所示,l为单摆的摆长,m为单摆摆球的质量.为了减小误差,三位同学在实验中每次测量单摆摆动30次(30T)的时间.丙同学在甲、乙同学实验的基础上继续实验,三位同学的实验数据分别记录在下表中.为了进一步探究单摆的摆动规律,他们进行了适量的运算,将结果记录在下表的后三列中.
(1)三位同学在实验中都要测量单摆摆动30个周期的用的时间,目的是______.
(2)分析比较实验序号1、2与3,可知甲同学得出的结论是:当单摆的摆长和摆动角度相同时,单摆的周期与摆球的质量______(选填“有关”、“无关”).
(3)分析比较实验序号4、5与6,可知乙同学研究的是:单摆的周期与摆球______的关系,他得出的结论是:当单摆的摆长和摆球质量相同时,单摆的周期与______.
(4)分析比较实验序号7、8与9中单摆的周期与摆长的关系,可知丙同学得出的结论是______.

| 同学 | 实验 序号 | l(米) | m(克) | θ(度) | 30T (秒) |
| 甲 | 1 | 1.0 | 30 | 4 | 60 |
| 2 | 1.0 | 40 | 4 | 60 | |
| 3 | 1.0 | 50 | 4 | 60 | |
| 乙 | 4 | 1.0 | 30 | 3 | 60 |
| 5 | 1.0 | 30 | 4 | 60 | |
| 6 | 1.0 | 30 | 5 | 60 | |
| 丙 | 7 | 0.8 | 30 | 4 | 54 |
| 8 | 1.0 | 40 | 4 | 60 | |
| 9 | 1.2 | 50 | 3 | 66 |
(2)分析比较实验序号1、2与3,可知甲同学得出的结论是:当单摆的摆长和摆动角度相同时,单摆的周期与摆球的质量______(选填“有关”、“无关”).
(3)分析比较实验序号4、5与6,可知乙同学研究的是:单摆的周期与摆球______的关系,他得出的结论是:当单摆的摆长和摆球质量相同时,单摆的周期与______.
(4)分析比较实验序号7、8与9中单摆的周期与摆长的关系,可知丙同学得出的结论是______.




