题目内容
 (2012?昌平区二模)有一个重为G的空心金属球A用弹簧秤吊着完全浸入一种液体中静止时,弹簧秤的示数为该金属球重力的
(2012?昌平区二模)有一个重为G的空心金属球A用弹簧秤吊着完全浸入一种液体中静止时,弹簧秤的示数为该金属球重力的| 1 |
| 5 |
| GS2 |
| S1 |
| GS2 |
| S1 |
分析:根据阿基米德原理求出金属球浸入第二种液体的体积,再求出由于金属球的浸入液面上升的高度,由液体压强公式求出液体压强的增加量,然后由压强公式的变形公式求出容器底所受液体压力的增加量.
解答:解:设金属球的体积是V,
金属球浸没在第一种液体时,
球排开液体的体积等于球的体积V,
此时弹簧秤的示数是球重的
,
则金属球受到的浮力F浮=G-
G=
G,
由阿基米德原理可知F浮=ρ1gV=
G,
所以G=
ρ1gV,
∵ρ1:ρ2=3:5,
∴G=
ρ1gV=
×
ρ2gV=
ρ2gV,
把金属球放入第二种液体,
设金属球受到的浮力等于它的重力时,金属球排开液体的体积是V排,
它受到的浮力F浮′=ρ2gV排=G=
ρ2gV,
则V排=
V,由此可见,金属球静止时将浮在液面上,
由于把金属球放入液体中,
液面上升的高度△h=
=
,
∵G=
ρ2gV,
∴V=
,
∴△h=
=
×
=
;
放入金属球后,液体对容器底部增加的压强△P=ρ2g△h=
,
∵P=
,
∴放入金属球后,容器底部所受液体的压力增大△F=△PS2=
.
故答案为:
.
金属球浸没在第一种液体时,
球排开液体的体积等于球的体积V,
此时弹簧秤的示数是球重的
| 1 |
| 5 |
则金属球受到的浮力F浮=G-
| 1 |
| 5 |
| 4 |
| 5 |
由阿基米德原理可知F浮=ρ1gV=
| 4 |
| 5 |
所以G=
| 5 |
| 4 |
∵ρ1:ρ2=3:5,
∴G=
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
把金属球放入第二种液体,
设金属球受到的浮力等于它的重力时,金属球排开液体的体积是V排,
它受到的浮力F浮′=ρ2gV排=G=
| 3 |
| 4 |
则V排=
| 3 |
| 4 |
由于把金属球放入液体中,
液面上升的高度△h=
| V排 |
| S1 |
| 3V |
| 4S1 |
∵G=
| 3 |
| 4 |
∴V=
| 4G |
| 3ρ2g |
∴△h=
| 3V |
| 4S1 |
| 3 |
| 4S1 |
| 4G |
| 3ρ2g |
| G |
| S1ρ2g |
放入金属球后,液体对容器底部增加的压强△P=ρ2g△h=
| G |
| S1 |
∵P=
| F |
| S |
∴放入金属球后,容器底部所受液体的压力增大△F=△PS2=
| GS2 |
| S1 |
故答案为:
| GS2 |
| S1 |
点评:本题考查了求液体对地面增大的压力,分析清楚图示情景、熟练应用浮力公式、阿基米德原理,认真计算即可正确解题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
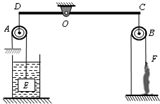 (2012?昌平区二模)在图所示的装置中OC:OD=2:1,A、B两个滑轮的质量均为2kg,E是边长为20cm、密度为ρ1的正方体合金块,当质量为60kg的人用F1=75N的力沿竖直方向向下拉绳时,合金块E全部浸没在密度为ρ2的液体中,杠杆恰好在水平位置平衡,此时人对地面的压强为
(2012?昌平区二模)在图所示的装置中OC:OD=2:1,A、B两个滑轮的质量均为2kg,E是边长为20cm、密度为ρ1的正方体合金块,当质量为60kg的人用F1=75N的力沿竖直方向向下拉绳时,合金块E全部浸没在密度为ρ2的液体中,杠杆恰好在水平位置平衡,此时人对地面的压强为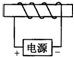 (2012?昌平区二模)在图中根据电源的正负极标出通电螺线管的N、S极.
(2012?昌平区二模)在图中根据电源的正负极标出通电螺线管的N、S极.