题目内容
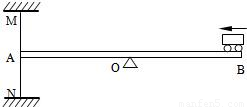
如图所示，均匀木板AB的长度为6m，它可绕位于其中央的支点O转动，左端A通过细绳MA、NA分别系在天花板、地面上．图示状态木板水平，细绳竖直且刚好绷紧．现使一玩具小汽车从B端开上木板，并以0.5m/s速度匀速前进．已知小汽车的功率为2W，质量1kg，g取10N/kg．求：（1）小汽车在木板上运动所受到的阻力的大小．
（2）从驶上木板开始计时，10s时被拉紧的细绳是哪段？拉力是多大？
分析：由杠杆平衡条件可以得到绳子拉力的方向，即可求出哪一段被拉紧；由汽车功率与运动的关系可以求出阻力，由运动学公式可求出10s时小车所在的位置，由力矩平衡可求出动力方向，及拉力的大小．
解答：解：（1）∵P=
=
=Fv，
∴小车的牵引力F=
=
=4N，
小车在水平方向受牵引力与摩擦力作用，小车做匀速直线运动，
处于平衡状态，由平衡条件得：摩擦力f=F=4N．
（2）∵v=
，
∴t=10s时，小车的移动的距离s=vt=0.5m/s×10=5m＞
=
=3m，
即小车已到O点的左侧，要想使杠杆平衡，杠杆左端绳子拉力应向上，即MA被拉紧，
此时L2=
-（L-s）=
-（6m-5m）=2m，
由杠杆平衡条件得：F1?L1=F2?L2，
则绳的拉力F1=
=
=
≈6.67N
答：（1）小车受阻力为4N．（2）绳MA被张紧，拉力为6.67N．
| W |
| t |
| Fs |
| t |
∴小车的牵引力F=
| P |
| v |
| 2W |
| 0.5m/s |
小车在水平方向受牵引力与摩擦力作用，小车做匀速直线运动，
处于平衡状态，由平衡条件得：摩擦力f=F=4N．
（2）∵v=
| s |
| t |
∴t=10s时，小车的移动的距离s=vt=0.5m/s×10=5m＞
| AB |
| 2 |
| 6m |
| 2 |
即小车已到O点的左侧，要想使杠杆平衡，杠杆左端绳子拉力应向上，即MA被拉紧，
此时L2=
| L |
| 2 |
| 6m |
| 2 |
由杠杆平衡条件得：F1?L1=F2?L2，
则绳的拉力F1=
| F2L2 |
| L1 |
| mgL2 |
| L1 |
| 1kg×10N/kg×2m |
| 3m |
答：（1）小车受阻力为4N．（2）绳MA被张紧，拉力为6.67N．
点评：本题结合了运动和杠杆平衡，题型较新，对此题应认真分析，对以后我们理解杠杆的平衡并加以应用是有帮助的．
练习册系列答案
相关题目
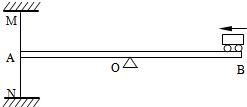如图所示，均匀木板AB的长度为6m，它可绕位于其中央的支点O转动，左端A通过细绳MA、NA分别系在天花板、地面上．图示状态木板水平，细绳竖直且刚好绷紧．现使一玩具小汽车从B端开上木板，并以0.5m/s速度匀速前进．已知小汽车的功率为4W，质量2kg，g取10N/kg．求：
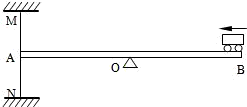如图所示，均匀木板AB的长度为6m，它可绕位于其中央的支点O转动，左端A通过细绳MA、NA分别系在天花板、地面上．图示状态木板水平，细绳竖直且刚好绷紧．现使一玩具小汽车从B端开上木板，并以0.5m/s速度匀速前进．已知小汽车的功率为4W，质量2kg，g取10N/kg．求：
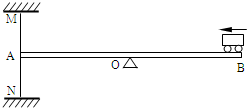如图所示，均匀木板AB的长度为6m，它可绕位于其中央的支点O转动，左端A通过细绳MA、NA分别系在天花板、地面上．图示状态木板水平，细绳竖直且刚好绷紧．现使一玩具小汽车从B端开上木板，并以0.5m/s速度匀速前进．已知小汽车的功率为2W，质量1kg，g取10N/kg．求：