题目内容
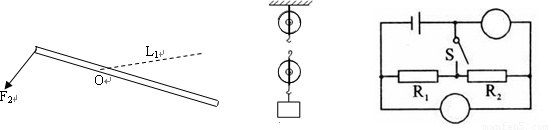
用如图所示的滑轮组吊起重物，不计绳重及摩擦．（1）当物重为150N时，绳端所用的拉力是60N，10s内重物被匀速提高2m时，求拉力F所做的功是多少？
（2）此时机械效率是多少？
（3）当所吊重物变为300N，完成上述过程时，机械效率会有变化吗？通过计算或推理说明理由．
分析：已知拉力、物体提升高度和绳子段数，可求总功，已知物重和高度可求有用功，根据公式算出机械效率．
解答：解：（1）W总=FS=3Fh=3×60N×2m=360J．
答：拉力F所做的功是360J．
（2）W有用=Gh=150N×2m=300J．
η=
=
= 83.3%．
答：此时机械效率是83.3%．
（3）W额=W总-W有用=360J-300J=60J，
W额=G动h ∴G动=
=
=30N，
η=
=
=
=91%
机械效率变大，证明物体越重，机械效率越高．
答：拉力F所做的功是360J．
（2）W有用=Gh=150N×2m=300J．
η=
| W有用 |
| W总 |
| 300J |
| 360J |
答：此时机械效率是83.3%．
（3）W额=W总-W有用=360J-300J=60J，
W额=G动h ∴G动=
| W额 |
| h |
| 60J |
| 2m |
η=
| W有用 |
| W总 |
| G1 |
| G1+ G动 |
| 300N |
| 300N+30N |
机械效率变大，证明物体越重，机械效率越高．
点评：本题考查机械效率的计算，属于比较简单的题．
练习册系列答案
相关题目
20、要用如图所示的滑轮组吊起重500N的重物．已知绳子能承受的最大拉力为200N，请画出绕绳的方法（不计滑轮重与摩擦）．
