题目内容
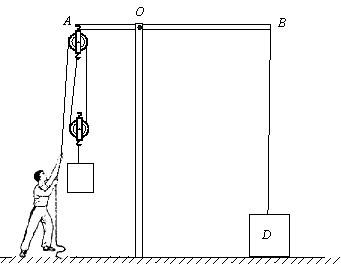
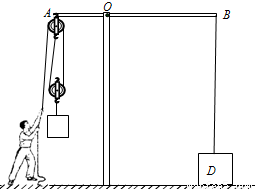
 图是工人提升物体的装置示意图,其中AB是一个不计重力、可以绕O点转动的杠杆,且AO:OB=2:5,杠杆B端系有重为1056N物体D,杠杆A端固定着滑轮组.质量为60kg的工人站在水平地面上,他对地面的压强p0=1.2×104Pa.当他利用该装置匀速提升重物M时,物体D受到的支持力为N1,工人对地面的压强p1=0.8×104Pa,此时滑轮组的机械效率η=90%;当工人利用该装置匀速提升重物N时,物体D受到的支持力为N2,工人竖直向下的拉力为F2;已知N1:N2=5:2,每个滑轮质量都相等,绳重及滑轮与轴的摩擦不计,g取10N/kg.求:
图是工人提升物体的装置示意图,其中AB是一个不计重力、可以绕O点转动的杠杆,且AO:OB=2:5,杠杆B端系有重为1056N物体D,杠杆A端固定着滑轮组.质量为60kg的工人站在水平地面上,他对地面的压强p0=1.2×104Pa.当他利用该装置匀速提升重物M时,物体D受到的支持力为N1,工人对地面的压强p1=0.8×104Pa,此时滑轮组的机械效率η=90%;当工人利用该装置匀速提升重物N时,物体D受到的支持力为N2,工人竖直向下的拉力为F2;已知N1:N2=5:2,每个滑轮质量都相等,绳重及滑轮与轴的摩擦不计,g取10N/kg.求:(1)提升重物M时工人竖直向下的拉力F1.
(2)提升重物N以0.5m/s的速度匀速上升时工人拉力的功率P.
分析:(1)利用人对地面产生的压强的变化,根据人的受力情况首先求出当提升物体M时人对滑轮组的拉力;
(2)当提升物体M时,分别以物体M、动滑轮、A端定滑轮、杠杆、配重D为研究对象进行受力分析,根据滑轮组的机械效率先求出物体M的重力和动滑轮的重力;然后根据力的平衡和杠杆的平衡条件列出等式,求得物体D受到的支持力为N1;
得出N1后根据已知N1:N2=5:2,求出N2,分析出当提升物体N时物体N、动滑轮、A端定滑轮、杠杆、配重D受力情况,再对以上物体根据力的平衡和杠杆的平衡条件逐步求出人得拉力F2、最后即可求功率P.
(2)当提升物体M时,分别以物体M、动滑轮、A端定滑轮、杠杆、配重D为研究对象进行受力分析,根据滑轮组的机械效率先求出物体M的重力和动滑轮的重力;然后根据力的平衡和杠杆的平衡条件列出等式,求得物体D受到的支持力为N1;
得出N1后根据已知N1:N2=5:2,求出N2,分析出当提升物体N时物体N、动滑轮、A端定滑轮、杠杆、配重D受力情况,再对以上物体根据力的平衡和杠杆的平衡条件逐步求出人得拉力F2、最后即可求功率P.
解答:解:当人站在地面上时受力分析如图1:
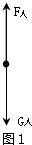
当提起物体M时各物体受力分析如图2:

当提起物体N时各物体受力分析如图3:

(1)由图受力分析可知:
对于人:G人=p0S人--------------①
G人=F1+p1S人------------②
则由①②式得:
=
=
=
=
;
∴F1=
G人=
×60kg×10N/kg=200N;
(2)提升物体M时,GM+G轮=2F1=2×200N=400N,
则η=
=
=
=90%,
解得:GM=360N,
则G轮=400N-GM=400N-360N=40N,
FA1=3F1+G轮=3×200N+40N=640N,
根据杠杆平衡条件得:
FA1L1=FB1L2,
FA1L1=(GD-N1)L2,
∴N1=GD-
FA1=1056N-
×640N=800N,
已知:N1:N2=5:2,
则N2=
×N1=
×800N=320N,
又FA2×L1=(GD-N2)×L2
FA2=
(GD-N2)=
×(1056N-320N)=1840N
FA2=3F2+G轮
F2=(FA2-G轮)/3=600N,
工人提升重物N以0.5m/s的速度匀速上升时的功率为:
P=F22v=600N×2×0.5m/s=600W.
答:(1)提升重物M时工人竖直向下的拉力F1为200N.
(2)提升重物N以0.5m/s的速度匀速上升时工人拉力的功率P为600W.

当提起物体M时各物体受力分析如图2:

当提起物体N时各物体受力分析如图3:

(1)由图受力分析可知:
对于人:G人=p0S人--------------①
G人=F1+p1S人------------②
则由①②式得:
| G人 |
| G人-F1 |
| p0S人 |
| p1S人 |
| p0 |
| p1 |
| 1.2×104Pa |
| 0.8×104Pa |
| 3 |
| 2 |
∴F1=
| 1 |
| 3 |
| 1 |
| 3 |
(2)提升物体M时,GM+G轮=2F1=2×200N=400N,
则η=
| W有用 |
| W总 |
| GMh |
| (GM+G轮)h |
| GM |
| 400N |
解得:GM=360N,
则G轮=400N-GM=400N-360N=40N,
FA1=3F1+G轮=3×200N+40N=640N,
根据杠杆平衡条件得:
FA1L1=FB1L2,
FA1L1=(GD-N1)L2,
∴N1=GD-
| L1 |
| L2 |
| 2 |
| 5 |
已知:N1:N2=5:2,
则N2=
| 2 |
| 5 |
| 2 |
| 5 |
又FA2×L1=(GD-N2)×L2
FA2=
| L2 |
| L1 |
| 5 |
| 2 |
FA2=3F2+G轮
F2=(FA2-G轮)/3=600N,
工人提升重物N以0.5m/s的速度匀速上升时的功率为:
P=F22v=600N×2×0.5m/s=600W.
答:(1)提升重物M时工人竖直向下的拉力F1为200N.
(2)提升重物N以0.5m/s的速度匀速上升时工人拉力的功率P为600W.
点评:本题为力学综合题,要求灵活利用所学知识、选用所学公式,利用好滑轮组的特点、杠杆平衡条件,能从图象得出相关信息是本题的关键,难题!

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目

 图是工人提升物体的装置示意图,其中AB是一个不计重力、可以绕O点转动的杠杆,且AO:OB=2:5,杠杆B端系有重为1056N物体D,杠杆A端固定着滑轮组.质量为60kg的工人站在水平地面上,他对地面的压强p0=1.2×104Pa.当他利用该装置匀速提升重物M时,物体D受到的支持力为N1,工人对地面的压强p1=0.8×104Pa,此时滑轮组的机械效率η=90%;当工人利用该装置匀速提升重物N时,物体D受到的支持力为N2,工人竖直向下的拉力为F2;已知N1:N2=5:2,每个滑轮质量都相等,绳重及滑轮与轴的摩擦不计,g取10N/kg.求:
图是工人提升物体的装置示意图,其中AB是一个不计重力、可以绕O点转动的杠杆,且AO:OB=2:5,杠杆B端系有重为1056N物体D,杠杆A端固定着滑轮组.质量为60kg的工人站在水平地面上,他对地面的压强p0=1.2×104Pa.当他利用该装置匀速提升重物M时,物体D受到的支持力为N1,工人对地面的压强p1=0.8×104Pa,此时滑轮组的机械效率η=90%;当工人利用该装置匀速提升重物N时,物体D受到的支持力为N2,工人竖直向下的拉力为F2;已知N1:N2=5:2,每个滑轮质量都相等,绳重及滑轮与轴的摩擦不计,g取10N/kg.求: