题目内容
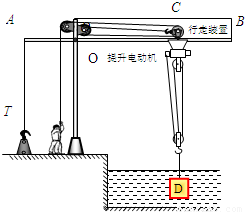
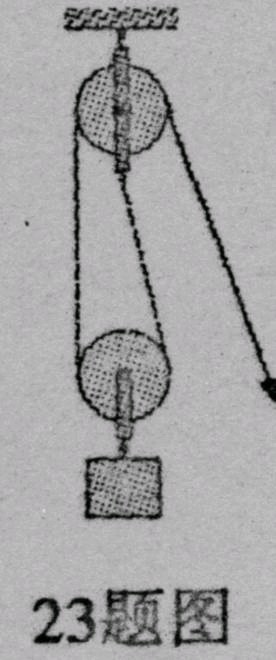
如图是某同学设计的简易打捞装置结构示意图.AOB是以O点为转轴,长为4m的轻质横梁,AB呈水平状态,AO=1m.在横梁上方行走装置可以在轨道槽内自由移动,行走装置下方固定有提升电动机.提升电动机通过细绳和滑轮组提起重物.固定在水平地面上的配重T通过细绳与横梁A端相连,GT=3000N.当行走装置处于C位置时,开始打捞物体D.质量m1是100kg、体积V为0.04m3物体D在水中匀速上升时,地面对配重T的支持力是N1,滑轮组的机械效率为75%;当物体D全部露出液面,滑轮组将物体D以v是0.1m/s的速度匀速竖直向上提升1m,此时地面对配重T的支持力是N2;N1:N2=5:1,若行走装置和提升电动机及定滑轮的总质量m2是20kg,忽略细绳与滑轮的摩擦以及水对物体的阻力,g取10N/kg.求:
(1)动滑轮的重力G动;
(2)物体D打捞出水面后,滑轮组的机械效率η2(结果保留两位小数);
(3)物体D打捞出水面后,电动机拉动细绳的功率P;
(4)OC的距离;
(5)此装置打捞物体D,物体D距O点的最大水平距离是多少?
【答案】分析:(1)因为AOC是一个杠杆,已知AO的长度,所以要求解OC的长度时,可以结合杠杆的平衡条件F1L1=F2L2进行求解,因此需要求出A点和C点的动力和阻力;
对配重T的受力分析可以求解动力FD1=F'D1,
对以行走装置、动滑轮M和物体D为研究对象,受力分析可以求解阻力FC1=F'C1,具体如下:
首先对物体D进行受力分析,物体D受到竖直向下的重力和竖直向上的水的浮力及绳子的拉力,在三个力的作用下处于平衡状态,即合外力为零,可以求出绳子拉力的大小;
然后结合滑轮组的机械效率公式进行推理求解计算出动滑轮的重力;
(2)对出水后物体及动滑轮进行分析,求出拉力的大小,知道物体D的质量,利用重力公式求D的重力,η=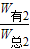 =
=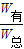 =
=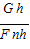 =
=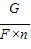 求此时滑轮组的机械效率;
求此时滑轮组的机械效率;
(3)求出绳端移动的速度,利用公式P=FV可求功率的大小;
(4)物体A在水中匀速上升过程中,以行走装置、动滑轮M和物体A为研究对象,进行受力分析,对杠杆上C点、D点受力分析、对配重T进行受力分析,得出各个物理量之间的等量关系,求出OC的距离;
(5)在C点受到的最大拉力等于m2g+G动+m1g,根据杠杆平衡条件求物体D距O点的最大水平距离.
解答:解:(1)物体D在水中匀速上升h1的过程中,
物体受到的浮力:
F浮=ρ水Vg=1.0×103kg/m3×0.04m3×10N/kg=400N,
滑轮组受到的阻力:
F1=mDg-F浮=100kg×10N/kg-400N=600N,
此时,滑轮组的机械效率η1=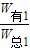 =
=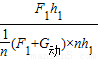 =
=
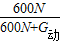 =75%,
=75%,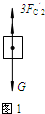
解得:G动=200N,
(2)对出水后物体及动滑轮进行分析如图(1)所示:
3FC2=G=G动+GD=mDg+200N=100kg×10N/kg+200N=1200N,
则FC2=400N,
此时,滑轮组的机械效率:
η2=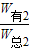 =
=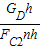 =
=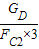 =
=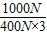 ≈83%;
≈83%;
(3)电动机拉动细绳的功率:
P=FC2×3v=400N×3×0.1m/s=120W;
(4)物体A在水中匀速上升过程中,以行走装置、动滑轮M和物体A为研究对象,受力分析图如图2所示,杠杆上C点、D点受力分析图如图3所示,配重T的受力分析图如图4所示.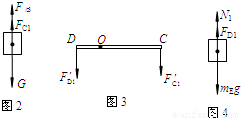
FC1=G-F浮
G=mg+G动+mAg,N1=mEg-FD1,F'D1?OD=F'C1?OC
FC1=F'C1,FD1=F'D1
得:N1=3000N-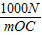
物体A离开水面后匀速上升的过程中,以行走装置、动滑轮M和物体A为研究对象,受力分析图如图5所示,配重E的受力分析图如图7所示,杠杆C点、D点受力分析图如图6所示.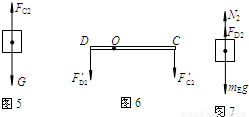
FC2=G,N2=mEg-FD2,F'D2?OD=F'C2?OC
FC2=F'C2,FD2=F'D2
N2=3000N-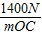
N1:N2=5:1
解得:OC=2m;
(5)由题知,GT×OA=(G1+m2g+G动)×OC最大,
即:3000N×1m=(1000N+200N+200N)×OC最大,
解得:OC最大≈2.14m.
答:(1)动滑轮的重力为200N;
(2)物体D打捞出水面后,滑轮组的机械效率为83%;
(3)物体D打捞出水面后,电动机拉动细绳的功率为120W;
(4)OC的距离为2m;
(5)此装置打捞物体D,物体D距O点的最大水平距离是2.14m.
点评:本题考查动滑轮重力、功率和距离的计算,关键是公式及其变形的灵活运用,难点是对物体进行受力分析,判断出动滑轮上绳子的段数,找出其中的等量关系.
对配重T的受力分析可以求解动力FD1=F'D1,
对以行走装置、动滑轮M和物体D为研究对象,受力分析可以求解阻力FC1=F'C1,具体如下:
首先对物体D进行受力分析,物体D受到竖直向下的重力和竖直向上的水的浮力及绳子的拉力,在三个力的作用下处于平衡状态,即合外力为零,可以求出绳子拉力的大小;
然后结合滑轮组的机械效率公式进行推理求解计算出动滑轮的重力;
(2)对出水后物体及动滑轮进行分析,求出拉力的大小,知道物体D的质量,利用重力公式求D的重力,η=
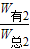 =
=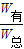 =
=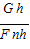 =
=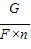 求此时滑轮组的机械效率;
求此时滑轮组的机械效率;(3)求出绳端移动的速度,利用公式P=FV可求功率的大小;
(4)物体A在水中匀速上升过程中,以行走装置、动滑轮M和物体A为研究对象,进行受力分析,对杠杆上C点、D点受力分析、对配重T进行受力分析,得出各个物理量之间的等量关系,求出OC的距离;
(5)在C点受到的最大拉力等于m2g+G动+m1g,根据杠杆平衡条件求物体D距O点的最大水平距离.
解答:解:(1)物体D在水中匀速上升h1的过程中,
物体受到的浮力:
F浮=ρ水Vg=1.0×103kg/m3×0.04m3×10N/kg=400N,
滑轮组受到的阻力:
F1=mDg-F浮=100kg×10N/kg-400N=600N,
此时,滑轮组的机械效率η1=
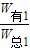 =
=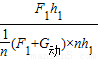 =
=
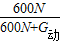 =75%,
=75%,
解得:G动=200N,
(2)对出水后物体及动滑轮进行分析如图(1)所示:
3FC2=G=G动+GD=mDg+200N=100kg×10N/kg+200N=1200N,
则FC2=400N,
此时,滑轮组的机械效率:
η2=
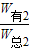 =
=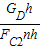 =
=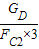 =
=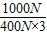 ≈83%;
≈83%;(3)电动机拉动细绳的功率:
P=FC2×3v=400N×3×0.1m/s=120W;
(4)物体A在水中匀速上升过程中,以行走装置、动滑轮M和物体A为研究对象,受力分析图如图2所示,杠杆上C点、D点受力分析图如图3所示,配重T的受力分析图如图4所示.

FC1=G-F浮
G=mg+G动+mAg,N1=mEg-FD1,F'D1?OD=F'C1?OC
FC1=F'C1,FD1=F'D1
得:N1=3000N-
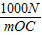
物体A离开水面后匀速上升的过程中,以行走装置、动滑轮M和物体A为研究对象,受力分析图如图5所示,配重E的受力分析图如图7所示,杠杆C点、D点受力分析图如图6所示.

FC2=G,N2=mEg-FD2,F'D2?OD=F'C2?OC
FC2=F'C2,FD2=F'D2
N2=3000N-
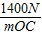
N1:N2=5:1
解得:OC=2m;
(5)由题知,GT×OA=(G1+m2g+G动)×OC最大,
即:3000N×1m=(1000N+200N+200N)×OC最大,
解得:OC最大≈2.14m.
答:(1)动滑轮的重力为200N;
(2)物体D打捞出水面后,滑轮组的机械效率为83%;
(3)物体D打捞出水面后,电动机拉动细绳的功率为120W;
(4)OC的距离为2m;
(5)此装置打捞物体D,物体D距O点的最大水平距离是2.14m.
点评:本题考查动滑轮重力、功率和距离的计算,关键是公式及其变形的灵活运用,难点是对物体进行受力分析,判断出动滑轮上绳子的段数,找出其中的等量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

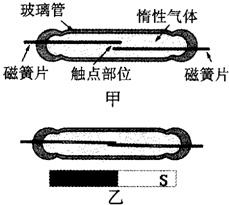 干簧管(也叫干簧继电器)比一般机械开关结构简单、体积小、速度高、工作寿命长;而与电子开关相比,它又有抗负载冲击能力强的特点,工作可靠性很高.如图甲所示为干簧管的结构简图,其中磁簧片是一种有弹性的薄铁片,被固定于玻璃管上.
干簧管(也叫干簧继电器)比一般机械开关结构简单、体积小、速度高、工作寿命长;而与电子开关相比,它又有抗负载冲击能力强的特点,工作可靠性很高.如图甲所示为干簧管的结构简图,其中磁簧片是一种有弹性的薄铁片,被固定于玻璃管上.

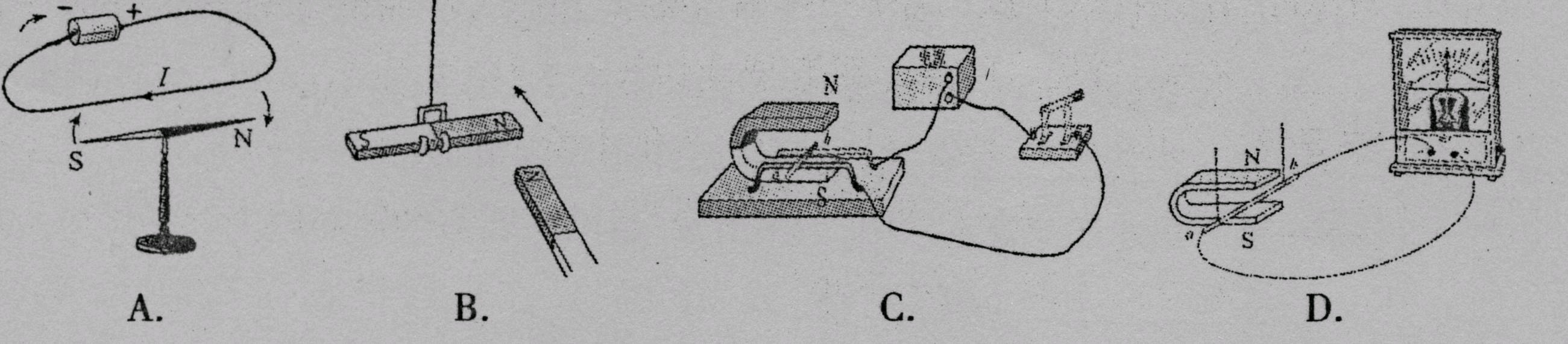
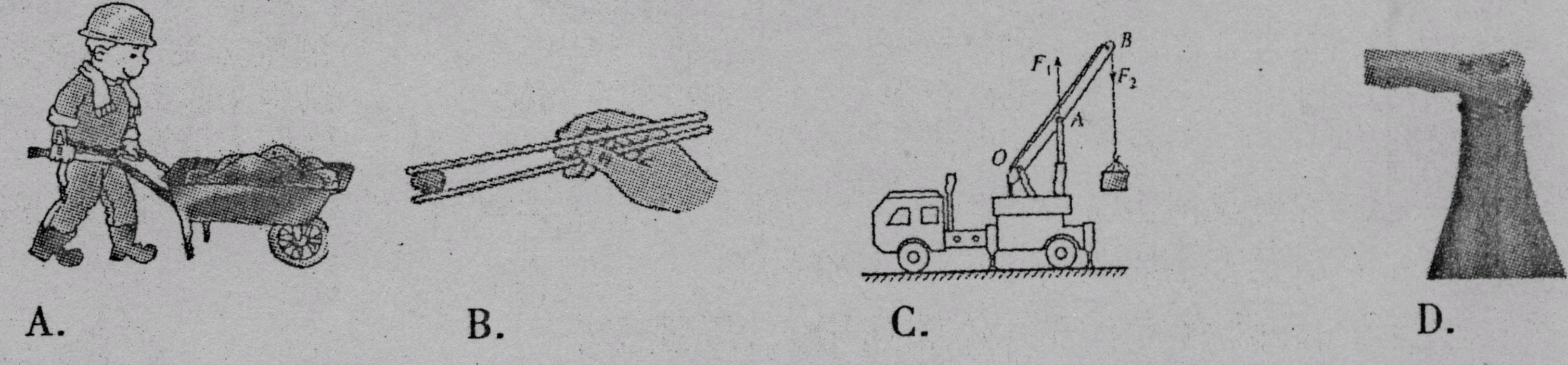
 5.关于光学器材或设备,下列说法错误的是.( )
5.关于光学器材或设备,下列说法错误的是.( )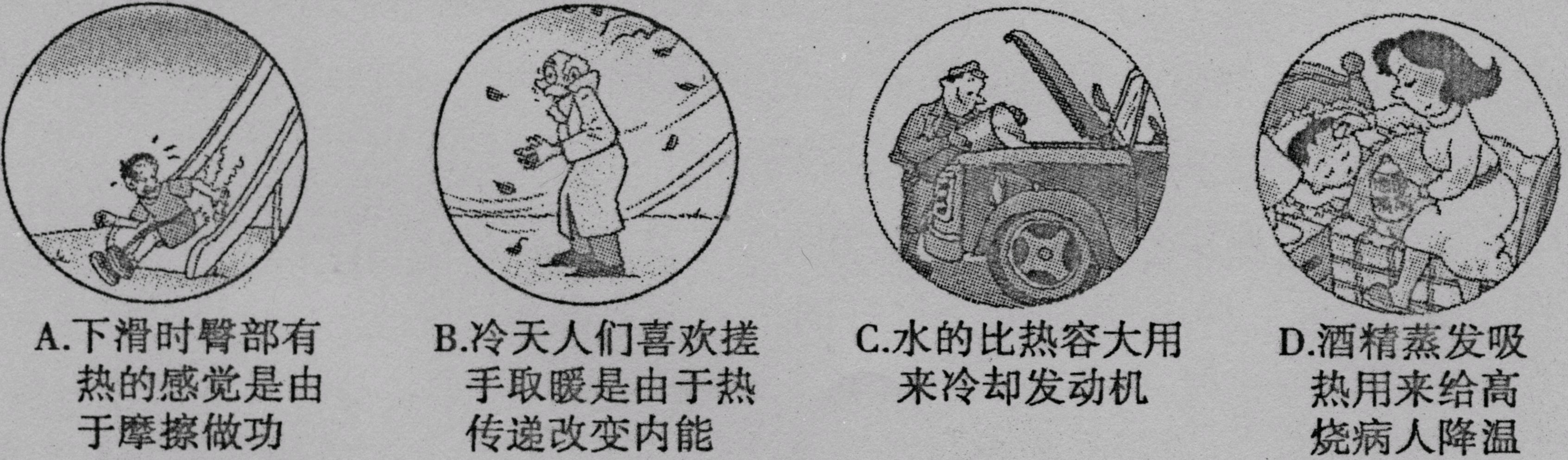


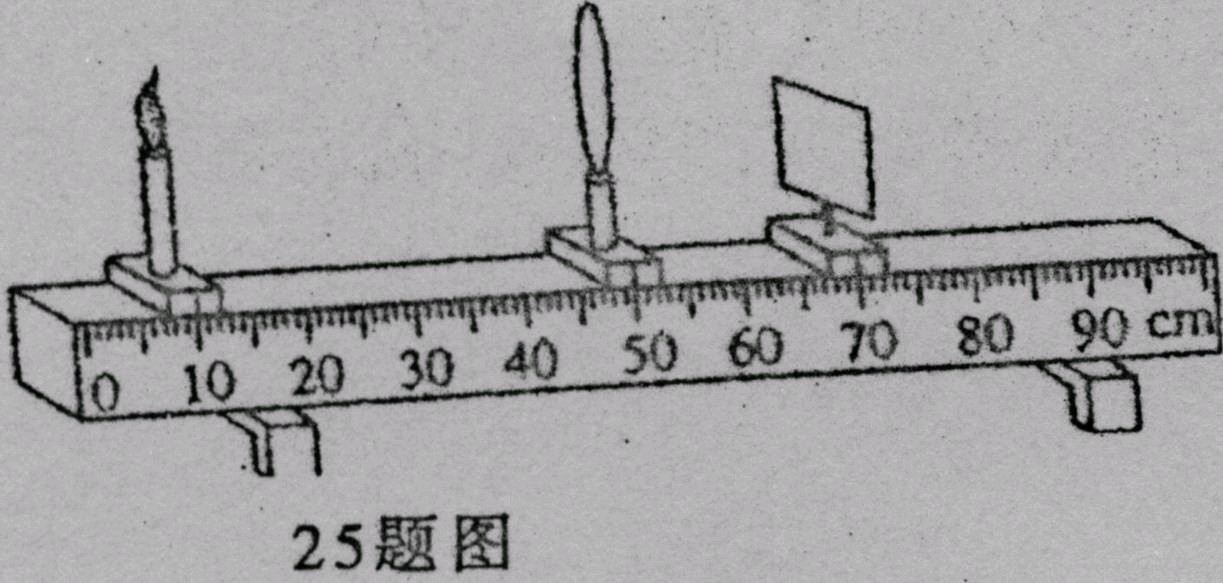
 25。如图所示,凸透镜的焦距为10cm,保持透镜位置不变,当蜡烛在10cm刻度处时,为了在光屏的中心找到像,应调整光屏的_______,并将光屏向_______方向移动(选填“远离透镜”或“靠近透镜").
25。如图所示,凸透镜的焦距为10cm,保持透镜位置不变,当蜡烛在10cm刻度处时,为了在光屏的中心找到像,应调整光屏的_______,并将光屏向_______方向移动(选填“远离透镜”或“靠近透镜").