题目内容
有两个质量相等的球，其体积之比V1：V2=1：5，密度之比ρ1：ρ2=4：1，其中一个球是空心的，已知实心球的体积为V，则空心球的空心部分的体积为（ ）
| A、2V | B、V | C、（1/5）V | D、（1/4）V |
分析：设这两个质量相等的球分别为甲球、乙球，由题可知：m甲=m乙；ρ甲：ρ乙=4：1，
就是说质量相等的情况下，体积比应该是1：4，但题目中有“其体积之比V1：V2=1：5，”
所以可知乙是空心的，可解得甲体积为V，乙实心体积为4V，
则空心球的空心部分的体积为乙球总体积减去实心部分体积即为空心部分体积，
就是说质量相等的情况下，体积比应该是1：4，但题目中有“其体积之比V1：V2=1：5，”
所以可知乙是空心的，可解得甲体积为V，乙实心体积为4V，
则空心球的空心部分的体积为乙球总体积减去实心部分体积即为空心部分体积，
解答：解：设这两个质量相等的球分别为甲球、乙球，由题可知：m甲=m乙；ρ甲：ρ乙=4：1，
所以有：
=
=
，V乙实=4V甲实，又因为有V甲：V乙=1：5 所以可以看出乙的体积比实心的变大了，所以乙球是空心的，甲是实心的，
所以有：V甲=V（甲实），V乙=5V甲，
所以空心球的空心部分的体积V空=V乙-V乙实=5V甲-4V甲=V甲=V．
故选B．
所以有：
| V甲实 |
| V乙实 |
| ||
|
| 1 |
| 4 |
所以有：V甲=V（甲实），V乙=5V甲，
所以空心球的空心部分的体积V空=V乙-V乙实=5V甲-4V甲=V甲=V．
故选B．
点评：此题主要考查空心混合物的密度计算，解答时除了灵活运用公式计算外，还要注意利用两球的质量相等和密度之比先判断出乙球是空心的，这是此题的突破点，也是此题的难点．
练习册系列答案
相关题目
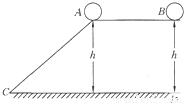
如图所示，有A，B两个质量相等的光滑金属球，放在同一水平面上．A沿高为h的光滑斜面滚下，B从h高处竖直落下，到达CD平面的D处，这时两球速度大小分别为νA和νB，则（ ）