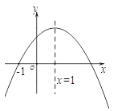【题目】初三某班同学小代想根据学习函数的经验，探究函数
的图象和性质，下面是他的探究过程，请补充完整：
（1）函数的自变量的取值范围是 ;
（2）下表是函数
与自变量
的几组对应值：
| -3 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | 7 |
| |
|
| 0.6 | m | 1 | 1.5 | 3 | n | 1.5 | 1 | 0.75 | 0.6 |
|
则m= ,n= ；
（3）在平面直角坐标系xoy中，补全此函数的图象:
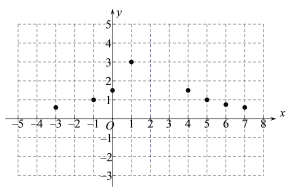
（4）根据函数图象，直接写出不等式
的解集 ;
（5）若函数与函数y＝x＋k图象有三个不同的交点，则k的取值范围是 .
【题目】蔬菜基地为选出适应市场需求的西红柿秧苗，在条件基本相同的情况下，将甲、乙两个品种的西红柿秧苗各500株种植在同一个大棚．对市场最为关注的产量进行了抽样调查，随机从甲、乙两个品种的西红柿秧苗中各收集了50株秧苗上的挂果数（西红柿的个数），并对数据（个数）进行整理、描述和分析，下面给出了部分信息.
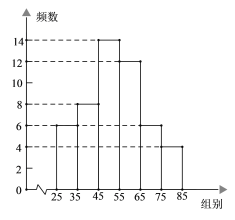
a. 甲品种挂果数频数分布直方图（数据分成6组：25≤x<35，35≤x<45，45≤x<55，55≤x<65，65≤x<75，75≤x<85）.
b. 甲品种挂果数在45≤x<55这一组的是：
45，45，46，47，47，49，49，49，49，50，50，51，51，54
c. 甲、乙品种挂果数的平均数、中位数、众数如下：
品种 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 49.4 | m | 49 | 1944.2 |
乙 | 48.6 | 48.5 | 47 | 3047 |
根据以上信息，回答下列问题:
(1)表中m= ；
(2)试估计甲品种挂果数超过49个的西红柿秧苗的数量；
(3)可以推断出 品种的西红柿秧苗更适应市场需求，理由为 （至少从两个不同的角度说明推断的合理性）.
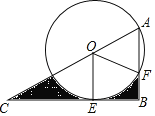
【题目】如图，Rt△ABC，∠B=90°，∠C=30°，O为AC上一点，OA=2，以O为圆心，以OA为半径的圆与CB相切于点E，与AB相交于点F，连接OE、OF，则图中阴影部分的面积是_______．
