【题目】小明研究一函数的性质，下表是该函数的几组对应值：
| ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ···· |
| ··· | 8 | 3 | 0 | -1 | 0 | 3 | 0 | -3 | -6 | ···· |
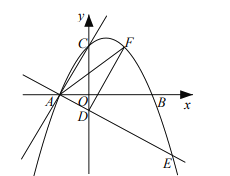
在平面直角坐标系中，描出以上表格中的各点，根据描出的点，画出该函数图象
根据所画函数图象，写出该函数的一条性质： ；
根据图像直接写出该函数的解析式及自变量的取值范围： ；
若一次函数
与该函数图像有三个交点，则
的范围是
【题目】某中学初三年级积极推进走班制教学．为了了解一段时间以来，“至善班”的学习效 果，年级组织了多次定时测试，现随机选取甲、乙两个“至善班”，从中各抽取
名同学在某一次定时测试中的数学成绩，其结果记录如下：
收集数据：
“至善班”甲班的名同学的数学成绩统计（满分为 100 分）（单位：分）
“至善班”乙班的名同学的数学成绩统计（满分为 100 分）（单位：分）
整理数据：（成绩得分用
表示）
分数 数量 班级 |
|
|
|
|
|
甲班（人数） | 1 | 3 | 4 | 6 | 6 |
乙班（人数） | 1 | 1 | 8 | 6 | 4 |
分析数据，并回答下列问题：
完成下表：
平均数 | 中位数 | 众数 | |
甲班 |
|
|
|
乙班 |
|
|
|
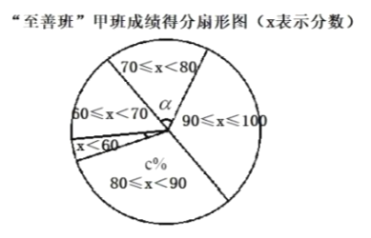
在“至善班”甲班的扇形图中， 成绩在
的扇形中，所对的圆心角
的度数为 ． 估计全部“至善班”的
人中优秀人数为 人．（
分及以上为优秀）．
根据以上数据，你认为“至善班” 班（填“甲”或“乙”）所选取做样本 的同学的学习效果更好一些，你所做判断的理由是：
①
②
