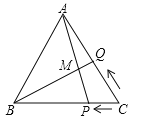
【题目】如图,等边![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 秒的速度由
秒的速度由![]() 向
向![]() 匀速运动,点
匀速运动,点![]() 从点
从点![]() 出发,以
出发,以![]() 秒的速度由
秒的速度由![]() 向
向![]() 匀速运动,
匀速运动,![]() 、
、![]() 交于点
交于点![]() ,当点
,当点![]() 到达
到达![]() 点时,
点时,![]() 、
、![]() 两点停止运动,设
两点停止运动,设![]() 、
、![]() 两点运动的时间为
两点运动的时间为![]() 秒,若
秒,若![]() 时,则
时,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】如图,等边![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 秒的速度由
秒的速度由![]() 向
向![]() 匀速运动,点
匀速运动,点![]() 从点
从点![]() 出发,以
出发,以![]() 秒的速度由
秒的速度由![]() 向
向![]() 匀速运动,
匀速运动,![]() 、
、![]() 交于点
交于点![]() ,当点
,当点![]() 到达
到达![]() 点时,
点时,![]() 、
、![]() 两点停止运动,设
两点停止运动,设![]() 、
、![]() 两点运动的时间为
两点运动的时间为![]() 秒,若
秒,若![]() 时,则
时,则![]() 的值是( )
的值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()