题目内容
(2009•无锡一模)已知:如图,抛物线y= x2+bx+c交y轴于点C,过抛物线上一点A(-3,-
x2+bx+c交y轴于点C,过抛物线上一点A(-3,- )作AM∥x轴,交抛物线于点B,交y轴于点M,连接AC、BC.
)作AM∥x轴,交抛物线于点B,交y轴于点M,连接AC、BC.(1)若S△ABC=2S△BMC,求这条抛物线对应的函数关系式;
(2)若P为(1)中的抛物线上的任一点,过点P作PQ⊥y轴于点Q,问:是否存在这样的点P,使得以A、B、P、Q为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.

【答案】分析:(1)根据等高三角形的面积比等于底边比可得出AB=2BM,即AM=3BM,由此可得出B点的坐标为(-1,- ),然后将A、B的坐标代入抛物线中即可求出这个二次函数的解析式.
),然后将A、B的坐标代入抛物线中即可求出这个二次函数的解析式.
(2)若使以A、B、P、Q为顶点的四边形是平行四边形,必须满足的条件是AB平行且相等于PQ,因此PQ=AB=2,即P点的横坐标的绝对值为2,然后将其代入抛物线的解析式中即可求出P点的值.
解答:解:(1)∵S△ABC=2S△BMC
∴AB=2BM
∴AB= AM=
AM= ×3=2
×3=2
∴B(-1,- )
)
把A、B点的坐标代入y= x2+bx+c,得:
x2+bx+c,得: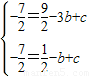 ,
,
解得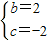 ,
,
∴y= x2+2x-2.
x2+2x-2.
(2)∵AB⊥y轴,PQ⊥y轴
∴AB∥PQ
∵AB、PQ为顶点的四边形是平行四边形.
∴PQ=AB=2
令x=2,y=y= ×22+2×2-2=4
×22+2×2-2=4
∴P1(2,4)
令x=-2,y=y= ×(-2)2+2×(-2)+-4
×(-2)2+2×(-2)+-4
∴P2(-2,-4).
点评:本题考查二次函数解析式的确定、图形的面积求法、平行四边形的判定和性质等知识及综合应用知识、解决问题的能力.
 ),然后将A、B的坐标代入抛物线中即可求出这个二次函数的解析式.
),然后将A、B的坐标代入抛物线中即可求出这个二次函数的解析式.(2)若使以A、B、P、Q为顶点的四边形是平行四边形,必须满足的条件是AB平行且相等于PQ,因此PQ=AB=2,即P点的横坐标的绝对值为2,然后将其代入抛物线的解析式中即可求出P点的值.
解答:解:(1)∵S△ABC=2S△BMC
∴AB=2BM
∴AB=
 AM=
AM= ×3=2
×3=2∴B(-1,-
 )
)把A、B点的坐标代入y=
 x2+bx+c,得:
x2+bx+c,得: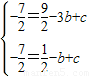 ,
,解得
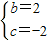 ,
,∴y=
 x2+2x-2.
x2+2x-2.(2)∵AB⊥y轴,PQ⊥y轴
∴AB∥PQ
∵AB、PQ为顶点的四边形是平行四边形.
∴PQ=AB=2
令x=2,y=y=
 ×22+2×2-2=4
×22+2×2-2=4∴P1(2,4)
令x=-2,y=y=
 ×(-2)2+2×(-2)+-4
×(-2)2+2×(-2)+-4∴P2(-2,-4).
点评:本题考查二次函数解析式的确定、图形的面积求法、平行四边形的判定和性质等知识及综合应用知识、解决问题的能力.

练习册系列答案
相关题目


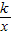 的图象上,则k= .
的图象上,则k= . cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合. 时,将Rt△ABC沿边AB向上翻折,并使点C与点C’重合,请求出翻折后Rt△ABC’与矩形DEFG重叠部分的周长.
时,将Rt△ABC沿边AB向上翻折,并使点C与点C’重合,请求出翻折后Rt△ABC’与矩形DEFG重叠部分的周长.