题目内容
(2010•大田县)已知抛物线y=ax2+bx+c(a≠0)经过点B(2,0)和点C(0,8),且它的对称轴是直线x=-2.(1)求抛物线与x轴的另一交点A的坐标;
(2)求此抛物线的解析式;
(3)连接AC,BC,若点E是线段AB上的一个动点(与点A,点B)不重合,过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.

【答案】分析:(1)知道对称轴了和x轴上另一点,就能求出该点.
(2)知道两点坐标和对称轴就能求出抛物线的解析式.
(3)依题意,AE=m,则BE=8-m,由题意可知△BEF∽△BAC,求出EF,过点F作FG⊥AB,垂是为G,则sin∠FEG=sin∠CAB,进而求出FG,由S=S△BCE-S△BFE,进而求得S与m之间的函数关系式.
(4)由S与m之间的函数关系式,求得S的最大值,算出点E坐标,判断三角形的形状.
解答:解:(1)∵抛物线y=ax2+bx+c的对称轴是直线x=-2,
∴由对称性可得A点的坐标为(-6,0);
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8.
将A(-6,0),B(2,0)代入表达式得
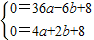 ,
,
解得 .
.
故所求解析式为y=- x2-
x2- x+8.
x+8.
(3)依题意,AE=m,则BE=8-m,
∵OA=6,OC=8,
∴AC=10,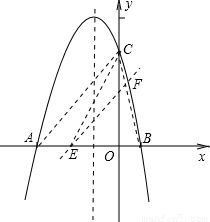
∵EF∥AC,
∴△BEF∽△BAC,
∴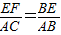 ,即EF=
,即EF=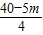 ,
,
过点F作FG⊥AB,垂是为G,则sin∠FEG=sin∠CAB= ,
,
∴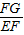 =
= ,
,
∴FG= ×
× =8-m,
=8-m,
∴S=S△BCE-S△BFE.
= (8-m)×8-
(8-m)×8- (8-m)(8-m),
(8-m)(8-m),
=- m2+4m,
m2+4m,
(4)存在.理由如下:
∵S=- m2+4m=-
m2+4m=- (m-4)2+8且-
(m-4)2+8且- <0,
<0,
∴当m=4时,S有最大值,S最大值=8,
∵m=4,
∴点E的坐标为(-2,0),
∴△BCE为等腰三角形.
点评:本题是二次函数的综合题,涉及到求抛物线的表达式和求最值等知识点,题不是很难,但要注意细节.
(2)知道两点坐标和对称轴就能求出抛物线的解析式.
(3)依题意,AE=m,则BE=8-m,由题意可知△BEF∽△BAC,求出EF,过点F作FG⊥AB,垂是为G,则sin∠FEG=sin∠CAB,进而求出FG,由S=S△BCE-S△BFE,进而求得S与m之间的函数关系式.
(4)由S与m之间的函数关系式,求得S的最大值,算出点E坐标,判断三角形的形状.
解答:解:(1)∵抛物线y=ax2+bx+c的对称轴是直线x=-2,
∴由对称性可得A点的坐标为(-6,0);
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8.
将A(-6,0),B(2,0)代入表达式得
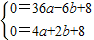 ,
,解得
 .
.故所求解析式为y=-
 x2-
x2- x+8.
x+8.(3)依题意,AE=m,则BE=8-m,
∵OA=6,OC=8,
∴AC=10,

∵EF∥AC,
∴△BEF∽△BAC,
∴
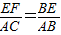 ,即EF=
,即EF=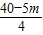 ,
,过点F作FG⊥AB,垂是为G,则sin∠FEG=sin∠CAB=
 ,
,∴
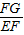 =
= ,
,∴FG=
 ×
× =8-m,
=8-m,∴S=S△BCE-S△BFE.
=
 (8-m)×8-
(8-m)×8- (8-m)(8-m),
(8-m)(8-m),=-
 m2+4m,
m2+4m,(4)存在.理由如下:
∵S=-
 m2+4m=-
m2+4m=- (m-4)2+8且-
(m-4)2+8且- <0,
<0,∴当m=4时,S有最大值,S最大值=8,
∵m=4,
∴点E的坐标为(-2,0),
∴△BCE为等腰三角形.
点评:本题是二次函数的综合题,涉及到求抛物线的表达式和求最值等知识点,题不是很难,但要注意细节.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
(2010•大田县)某中学篮球队12名队员的年龄情况如下:
则这个队队员年龄的众数和中位数分别是( )
A.15,16
B.15,15
C.15,15.5
D.16,15
| 年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
A.15,16
B.15,15
C.15,15.5
D.16,15